
����Ŀ����P1 �� P2 �� ��PnΪƽ����ڵ�n���㣬��ƽ����ڵ����е��У�����P����P1 �� P2 �� ��Pn�ľ���֮����С����Ƶ�PΪP1 �� P2 �� ��Pn��һ������λ�㡱�����磬�߶�AB�ϵ�����㶼�Ƕ˵�A��B����λ�㣬�����������⣺
����������A��B��C���ߣ�C���߶�AB�ϣ���C��A��B��C����λ�㣻
��ֱ��������б�ߵ��е��Ǹ�ֱ�������������������λ�㣻
�����ĸ���A��B��C��D���ߣ������ǵ���λ�������Ψһ��
�����ζԽ��ߵĽ����Ǹ������ĸ������Ψһ��λ�㣮
���е�����������д���������������ţ���
���𰸡��٢�
���������⣺����������A��B��C���ߣ���C���߶�AB�ϣ����߶�AB����һ�㶼Ϊ����λ�㡱��CҲ�����⣬��C��A��B��C����λ�㣬����ȷ��
�ھ�һ����������߳�Ϊ3��4��5��ֱ��������ABC����ֱ�������ε�б�ߵ��е㵽��������ľ���֮��Ϊ5+2.5=7.5����ֱ�Ƕ��㵽��������ľ���֮��Ϊ7������ֱ��������б�ߵ��е㲻�Ǹ�ֱ�������������������λ�㣬�ʢڴ���
�����ĸ���A��B��C��D���ߣ������ǵ���λ�����м��������߶��ϵ�����һ���㣬�����ǵ���λ����ڵ���Ψһ���ʢ۴���
����ͼ��������ABCD�У��Խ��ߵĽ���O��P������һ�㣬���������������֮�ʹ��ڵ����ߵ�
PA+PB+PC+PD��AC+BD=OA+OB+OC+OD���������ζԽ��ߵĽ����Ǹ������ĸ������Ψһ��λ�㣬�ʢ���ȷ��
���Դ��ǣ��٢ܣ�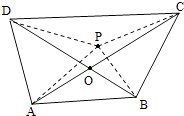
�����㾫����ͨ������������������ж���Ӧ�ã������������⻥Ϊ������⣬��������ͬ������ԣ���������Ϊ������������⣬���ǵ������û�й�ϵ�����Խ����⣮


 ������������Ӧ����ϵ�д�
������������Ӧ����ϵ�д� ͬ����չ�Ķ�ϵ�д�
ͬ����չ�Ķ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������������![]() �ĵײ�����ͬһ��ˮƽ�������Ҿ���ˮƽ�洹ֱ�����ǵĸ߶ȷֱ���9
�ĵײ�����ͬһ��ˮƽ�������Ҿ���ˮƽ�洹ֱ�����ǵĸ߶ȷֱ���9![]() ��15
��15![]() ���ӽ�����
���ӽ�����![]() �Ķ���
�Ķ���![]() ��������
��������![]() ���ӽ�
���ӽ�![]() ��
��

��1����![]() �ij��ȣ�
�ij��ȣ�
��2�����߶�![]() ��ȡһ��
��ȡһ��![]() ��
��![]() ���
���![]() ���غ������ӵ�
���غ������ӵ�![]() ����������������ӽǷֱ�Ϊ
����������������ӽǷֱ�Ϊ![]() �ʵ�
�ʵ�![]() �ںδ�ʱ��
�ںδ�ʱ��![]() ��С��
����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������f��x��ͬʱ���㣺
�ٶ��ڶ������ϵ�����x����f��x��+f����x����0��
�ڶ��ڶ������ϵ�����x1��x2����x1��x2ʱ������![]() 0����ƺ���f��x��Ϊ�����뺯������
0����ƺ���f��x��Ϊ�����뺯������
���������ĸ������Т�f��x��![]() �� ��f��x��
�� ��f��x��![]() �� ��f��x��
�� ��f��x��![]() ����f��x��
����f��x��![]() ��
��
�ܱ���Ϊ�����뺯��������_______________������Ӧ����ţ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��������ʵ��x��y����f��x+y��=f��x��+f��y���ҵ�x��0��f��x����0��
���������ĸ����ۣ�
��f��0��=0����f��x��Ϊż������
��f��x��ΪR�ϼ���������f��x��ΪR����������
������ȷ�Ľ����ǣ�������
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ������������ԭ��
������������ԭ��![]() ��������
��������![]() ���ϣ�����һ������ǡ����������
���ϣ�����һ������ǡ����������![]() �Ľ��㣬������������˫����
�Ľ��㣬������������˫����![]() �������ʵĵ���.
�������ʵĵ���.
��������Բ![]() �ı����̣�
�ı����̣�
������Բ![]() ���ҽ���
���ҽ���![]() ��ֱ��
��ֱ��![]() ����Բ
����Բ![]() ��
��![]() ��
��![]() ���㣬��
���㣬��![]() ����
����![]() �㣬��
�㣬��![]() ��
��![]() ����֤��
����֤��![]() Ϊ��ֵ.
Ϊ��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Ԫ263�����ң��ҹ���ѧ�����շ��ֵ�Բ�ڽ�������εı�����������ʱ������ε���������ӽ�Բ��������������ˡ���Բ���������á���Բ���������յõ���Բ���ʾ�ȷ��С�������λ�Ľ���ֵ3.14,����������ġ����ʡ����������յġ���Բ����˼����Ƶ�һ�������ͼ���������ֵΪ�� ��
���ο����ݣ�![]() ��
��

A. 12 B. 24 C. 48 D. 96
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijͬѧΪ�о�����![]() �����ʣ���������ͼ��ʾ�������߳�Ϊ1��������ABCD��BEFC����P�DZ�BC�ϵ�һ�����㣬��
�����ʣ���������ͼ��ʾ�������߳�Ϊ1��������ABCD��BEFC����P�DZ�BC�ϵ�һ�����㣬��![]() ����
����![]() ������ο���Щ��Ϣ����֪����
������ο���Щ��Ϣ����֪����![]() ��ͼ��ĶԳ�����______������
��ͼ��ĶԳ�����______������![]() �����ĸ�����______��
�����ĸ�����______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ�еĹ������̣����������Ʒ����Ҫ����_______���ӹ��ͼ�������·�Ʒ�IJ�����______�ֲ�ͬ������
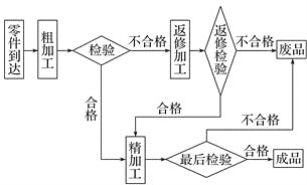
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com