
已知一个四面体其中五条棱的长分别为1,1,1,1,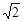 ,则此四面体体积的最大值是
,则此四面体体积的最大值是
A.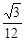 | B.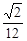 | C.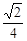 | D.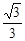 |
A
解析试题分析:设四面体为P-ABC,则设PC=X,AB=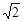 ,其余的各边为1,那么取AB的中点D,那么连接PD,因此可知,AB垂直与平面PCD,则棱锥的体积可以运用以PCD为底面,高为AD,BD的两个三棱锥体积的和来表示,因此只要求解底面积的最大值即可。由于PD=CD=
,其余的各边为1,那么取AB的中点D,那么连接PD,因此可知,AB垂直与平面PCD,则棱锥的体积可以运用以PCD为底面,高为AD,BD的两个三棱锥体积的和来表示,因此只要求解底面积的最大值即可。由于PD=CD= ,那么可知三角形PDC的面积越大,体积越大,因此可知面积的最大值为
,那么可知三角形PDC的面积越大,体积越大,因此可知面积的最大值为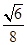 ,也就是当PD垂直于CD时,面积最大,因此可四面体的体积的最大值为
,也就是当PD垂直于CD时,面积最大,因此可四面体的体积的最大值为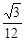 ,选A.
,选A.
考点:考查了多面体体积的运用。
点评:解决该试题的关键是对于四面体的边长的合理布置,然后进行作相应的辅助线,来借助于垂直的性质,表示多面体的体积,进而得到表达式,结合函数来求解最值,属于中档题。


科目:高中数学 来源: 题型:单选题
我国齐梁时代的数学家祖暅(公元前5-6世纪)提出了一条原理:“幂势既同,则积不容异.”这句话的意思是:夹在两个平行平面间的两个几何体,被平行于这两个平行平面的任何平面所截,如果截得的两个截面的面积总是相等,那么这两个几何体的体积相等.
设:由曲线 和直线
和直线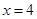 ,
,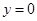 所围成的平面图形,绕
所围成的平面图形,绕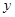 轴旋转一周所得到的旋转体为
轴旋转一周所得到的旋转体为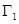 ;由同时满足
;由同时满足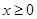 ,
,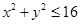 ,
,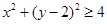 ,
,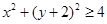 的点
的点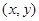 构成的平面图形,绕
构成的平面图形,绕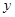 轴旋转一周所得到的旋转体为
轴旋转一周所得到的旋转体为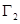 .根据祖暅原理等知识,通过考察
.根据祖暅原理等知识,通过考察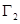 可以得到
可以得到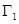 的体积为
的体积为
A.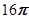 | B.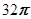 | C.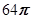 | D.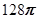 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com