
【题目】如图,矩形![]() 平面
平面![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点.
的中点.
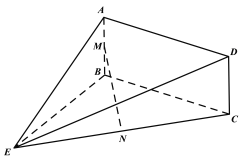
(1)证明:![]() 平面
平面![]() ;
;
(2)若![]() ,求二面角
,求二面角![]() 的大小.
的大小.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)取DE中点F,分别连结AF,FN,证明![]() ,再利用线面平行的判定定理证明线面平行;
,再利用线面平行的判定定理证明线面平行;
(2)以B为原点建立空间直角坐标系![]() ,得则
,得则![]() ,
,![]() ,
,![]() ,
,![]() ,求出
,求出![]() 为平面ABCD的一个法向量,
为平面ABCD的一个法向量,![]() 为平面AED的法向量,从而求得二面角
为平面AED的法向量,从而求得二面角![]() 的大小.
的大小.
(1)证明:取DE中点F,分别连结AF,FN
又N为BC中点,
所以![]() ,
,
因为矩形ABCD中,M为AB的中点,
所以![]()
所以![]() ,
,
所以四边形AMNF为平行四边形,
所以![]() ,
,
又因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
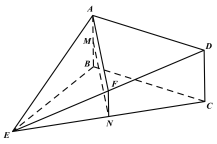
(2)因为矩形![]() 平面
平面![]() ,
,
矩形![]() 平面
平面![]() ,
, ![]()
所以![]() 平面
平面![]() .
.
如图,以B为原点建立空间直角坐标系![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
因为![]() 轴
轴![]() 平面ABCD,
平面ABCD,
所以![]() 为平面ABCD的一个法向量,
为平面ABCD的一个法向量,
设![]() 为平面AED的法向量,
为平面AED的法向量,
因为![]() ,
,![]() ,
,
所以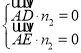 ,得
,得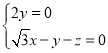 ,
,
故可取![]() ,
,
则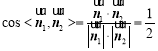 ,
,
由图可知二面角的平面角为锐角,
所以二面角![]() 的大小为
的大小为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在一个有穷数列每相邻两项之间添加一项,使其等于两相邻项的和,我们把这样的操作叫做该数列的一次“H扩展”. 已知数列1,2. 第一次“H扩展”后得到1,3,2;第二次“H扩展”后得到1,4,3,5,2; 那么第10次“H扩展”后得到的数列的所有项的和为( )
A.88572B.88575C.29523D.29526
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由无理数引发的数学危机一直延续到19世纪,直到1872年,德国数学家戴德金提出了“戴德金分割”,才结束了持续2000多年的数学史上的第一次大危机.所谓戴德金分割,是指将有理数集![]() 划分为两个非空的子集
划分为两个非空的子集![]() 与
与![]() ,且满足
,且满足![]() ,
,![]() ,
,![]() 中的每一个元素都小于
中的每一个元素都小于![]() 中的每一个元素,则称
中的每一个元素,则称![]() 为戴德金分割.试判断,对于任一戴德金分割
为戴德金分割.试判断,对于任一戴德金分割![]() ,下列选项中不可能成立的是
,下列选项中不可能成立的是
A.![]() 没有最大元素,
没有最大元素,![]() 有一个最小元素
有一个最小元素
B.![]() 没有最大元素,
没有最大元素,![]() 也没有最小元素
也没有最小元素
C.![]() 有一个最大元素,
有一个最大元素,![]() 有一个最小元素
有一个最小元素
D.![]() 有一个最大元素,
有一个最大元素,![]() 没有最小元素
没有最小元素
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年1月14日,国防科工局宣布,嫦娥四号任务已经通过了探月工程重大专项领导小组审议通过,正式开始实施.如图所示,假设“嫦娥四号”卫星将沿地月转移轨道飞向月球后,在月球附近一点P变轨进入以月球球心F为一个焦点的椭圆轨道Ⅰ绕月飞行,之后卫星在P点第二次变轨进入仍以F为一个焦点的椭圆轨道Ⅱ绕月飞行.若用2c1和2c2分别表示椭圆轨道Ⅰ和Ⅱ的焦距,用2a1和2a2分别表示椭圆轨道Ⅰ和Ⅱ的长轴长,给出下列式子:
①a1+c1=a2+c2; ②a1-c1=a2-c2; ③c1a2>a1c2. ④![]()
其中正确式子的序号是( )
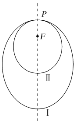
A.①③B.②③C.①④D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一种掷硬币走跳棋的游戏:在棋盘上标有第1站、第2站、第3站、…、第100站,共100站,设棋子跳到第![]() 站的概率为
站的概率为![]() ,一枚棋子开始在第1站,棋手每掷一次硬币,棋子向前跳动一次.若硬币的正面向上,棋子向前跳一站;若硬币的反面向上,棋子向前跳两站,直到棋子跳到第99站(失败)或者第100站(获胜)时,游戏结束.
,一枚棋子开始在第1站,棋手每掷一次硬币,棋子向前跳动一次.若硬币的正面向上,棋子向前跳一站;若硬币的反面向上,棋子向前跳两站,直到棋子跳到第99站(失败)或者第100站(获胜)时,游戏结束.
(1)求![]()
![]()
![]() ;
;
(2)求证:数列![]()
![]() 为等比数列;
为等比数列;
(3)求玩该游戏获胜的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() (
(![]() 、
、![]() 为实常数).
为实常数).
(1)当![]() 时,证明:
时,证明:![]() 不是奇函数;
不是奇函数;
(2)设![]() 是奇函数,求
是奇函数,求![]() 与
与![]() 的值;
的值;
(3)当![]() 是奇函数时,研究是否存在这样的实数集的子集
是奇函数时,研究是否存在这样的实数集的子集![]() ,对任何属于
,对任何属于![]() 的
的![]() 、
、![]() ,都有
,都有![]() 成立?若存在试找出所有这样的
成立?若存在试找出所有这样的![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
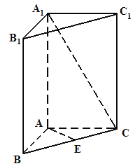
【题目】如图,直三棱柱![]() 的底面
的底面![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,侧棱
,侧棱![]() 底面
底面![]() ,且
,且![]() ,
,![]() 是
是![]() 的中点.
的中点.
(1)求直三棱柱![]() 的全面积;
的全面积;
(2)求异面直线![]() 与
与![]() 所成角
所成角![]() 的大小(结果用反三角函数表示);
的大小(结果用反三角函数表示);
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com