
 ,一旦发生,将造成某公司300万元的损失.现有甲、乙两种相互独立的预防措施可供选择,单独采用甲、乙预防措施所需的费用分别为40万元和20万元,采用相应预防措施后此突发事件不发生的概率分别为
,一旦发生,将造成某公司300万元的损失.现有甲、乙两种相互独立的预防措施可供选择,单独采用甲、乙预防措施所需的费用分别为40万元和20万元,采用相应预防措施后此突发事件不发生的概率分别为 和
和 .若预防方案允许甲、乙两种预防措施单独采用、同时采用或都不采用,请分别计算这几种预防方案的总费用,并指出哪一种预防方案总费用最少.
.若预防方案允许甲、乙两种预防措施单独采用、同时采用或都不采用,请分别计算这几种预防方案的总费用,并指出哪一种预防方案总费用最少. (万元) . …………2分
(万元) . …………2分 万元,发生突发事件的概率为
万元,发生突发事件的概率为 ,损失期望值为
,损失期望值为 (万元), …………4分
(万元), …………4分 (万元) . …………5分
(万元) . …………5分 万元,发生突发事件的概率为
万元,发生突发事件的概率为 ,损失期望值为
,损失期望值为 (万元), …………7分
(万元), …………7分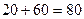 (万元) . …………8分
(万元) . …………8分 万元,发生突发事件的概率为
万元,发生突发事件的概率为 , …………10分
, …………10分 (万元), …………11分
(万元), …………11分 (万元). …………12分
(万元). …………12分

 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:高中数学 来源:不详 题型:解答题
 数依次为:60,65,70,75,80,85,90,95;
数依次为:60,65,70,75,80,85,90,95; 为这8位同学中数学和物理分数均为优秀的人数,求
为这8位同学中数学和物理分数均为优秀的人数,求 的分布列和数学期望;
的分布列和数学期望;| 学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
数学分数 | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 |
物理分数 | 72 | 77 | 80 | 84 | 88 | 90 | 93 | 95 |
 与
与 之间具有较强的线性相关关系,求出
之间具有较强的线性相关关系,求出 与
与 的线性回归方程(系数精确到0.01).(参考公式:
的线性回归方程(系数精确到0.01).(参考公式: ,其中
,其中 ,
, ;参考数据:
;参考数据: ,
, ,
, ,
, ,
, ,
, ,
, )
)查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 的分布列及数学期望;
的分布列及数学期望;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 3个旅游团提供甲、乙、丙、丁4条旅游线路,每个旅游团从中任选一条。
3个旅游团提供甲、乙、丙、丁4条旅游线路,每个旅游团从中任选一条。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com