
 ,乙的成绩不低于8.5的概率为
,乙的成绩不低于8.5的概率为 .所求事件的概率等于甲仅有一次成绩不低于8.5、乙也仅有一次成绩不低于8.5的概率,加上甲有2次成绩都不低于8.5而乙2次成绩都低于8.5的概率,再加上甲2次成绩都低于8.5而乙2次成绩都不低于8.5的概率.
.所求事件的概率等于甲仅有一次成绩不低于8.5、乙也仅有一次成绩不低于8.5的概率,加上甲有2次成绩都不低于8.5而乙2次成绩都低于8.5的概率,再加上甲2次成绩都低于8.5而乙2次成绩都不低于8.5的概率. .
. .
. .
. ,乙的成绩不低于8.5的概率为
,乙的成绩不低于8.5的概率为 .
. .
. .
.

科目:高中数学 来源: 题型:
| 2 |
| 3 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2011-2012学年四川省绵阳市高三第二次月考理科数学试卷 题型:解答题
为备战2012年伦敦奥运会,爾家篮球队分轮次迸行分项冬训.训练分为甲、乙两组,根据经验,在冬训期间甲、乙两组完成各项训练任务的概率分别为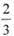 和P(P>0)假设每轮训练中两组都各有两项训练任务需完成,并且每项任务的完成与否互不影响.若在一轮冬训中,两组完成训练任务的项数相等且都不小于一项,则称甲、乙两组为“友好组”
和P(P>0)假设每轮训练中两组都各有两项训练任务需完成,并且每项任务的完成与否互不影响.若在一轮冬训中,两组完成训练任务的项数相等且都不小于一项,则称甲、乙两组为“友好组”
(I)若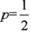 求甲、乙两组在完成一轮冬训中成为“友好组”的概率;
求甲、乙两组在完成一轮冬训中成为“友好组”的概率;
(II)设在6轮冬训中,甲、乙两组成为“友好组”的次数为 ,当
,当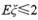 时,求P的取值范围.
时,求P的取值范围.
查看答案和解析>>
科目:高中数学 来源:2012年四川省绵阳市高考数学二模试卷(理科)(解析版) 题型:解答题
 和P(P>0)假设每轮训练中两组都各有两项训练任务需完成,并且每项任务的完成与否互不影响.若在一轮冬训中,两组完成训练任务的项数相等且都不小于一项,则称甲、乙两组为“友好组”
和P(P>0)假设每轮训练中两组都各有两项训练任务需完成,并且每项任务的完成与否互不影响.若在一轮冬训中,两组完成训练任务的项数相等且都不小于一项,则称甲、乙两组为“友好组” 求甲、乙两组在完成一轮冬训中成为“友好组”的概率;
求甲、乙两组在完成一轮冬训中成为“友好组”的概率;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com