
分析 (1)an+1=2an+3an-1(n≥2).可得到an+1+an=3(an+an-1),问题得以证明,
(2)通过an+1=2an+3an-1(n≥2).变形为an+1+λan=m(an+λan-1)形式计算可求.
解答 解:(1)∵数列{an}中,a1=2,a2=3,且an+1=2an+3an-1(n≥2)
∴an+1+an=3(an+an-1),
又a2+a1=5,
∴{an+1+an}是首项为5,公比为3的等比数列,
∵bn=an+1+an,
∴{bn}是等比数列,
(2)由(1)可得an+1+an=5×3n-1,①
∵an+1=2an+3an-1,
∴an+1-3an=-(an-3an-1),
又∵a2-3a1=3-3×2=-3,
∴数列{an+1-3an}是以-3为首项、-1为公比的等比数列,
∴an+1-3an=-3•(-1)n-1,②
由①②可得an=$\frac{1}{4}$(5×3n-1+3×(-1)n-1)
点评 本题考查数列的通项,对表达式的灵活变形是解决本题的关键,注意解题方法的积累,属于中档题


科目:高中数学 来源: 题型:解答题
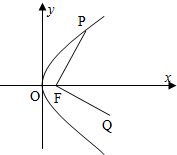 如图,点P是抛物线y2=4x上动点,F为抛物线的焦点,将向量$\overrightarrow{FP}$绕点F按顺时针方向旋转90°到$\overrightarrow{FQ}$
如图,点P是抛物线y2=4x上动点,F为抛物线的焦点,将向量$\overrightarrow{FP}$绕点F按顺时针方向旋转90°到$\overrightarrow{FQ}$查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1)∪(1,+∞) | B. | (-∞,-1)∪(0,1) | C. | (-1,0)∪(0,1) | D. | (-1,0)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\frac{π}{12},0)$ | B. | $(\frac{5π}{12},0)$ | C. | $(-\frac{5π}{12},0)$ | D. | $(\frac{π}{6},0)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
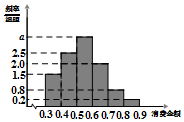 某电商对10000名网购者2015年度消费情况进行统计,其消费频率分布直方图如图,则在这些网购者中,消费金额在[0.5,0.9]内的人数为( )
某电商对10000名网购者2015年度消费情况进行统计,其消费频率分布直方图如图,则在这些网购者中,消费金额在[0.5,0.9]内的人数为( )| A. | 2000 | B. | 4500 | C. | 6000 | D. | 7500 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com