
分析 (Ⅰ)求出函数的导数,得到函数的单调区间,从而求出函数的极小值即可;
(Ⅱ)通过讨论a的范围,判断函数的单调性,从而求出函数的极大值和极小值,判断出函数的零点个数即可.
解答 解:(Ⅰ) f′(x)=3x2-9x+6=3(x-2)(x-1),
当x<1或x>2,f(x)在(-∞,1)和(2,+∞)上递增,
f(x)在(1,2)上递减,
所以f(x)极小值为f(2)=-1…(5分)
(Ⅱ) ①若a=0时,则f(x)=-3(x-1)2,
∴f(x)的图象与x轴只有一个交点;
②若a<0时,则$\frac{2}{a}<1$,
∵${f^'}(x)=3a{x^2}-3(a+2)x+6=3a(x-\frac{2}{a})(x-1)$,
当x>1或$x<\frac{2}{a}$时,f'(x)<0;
当$\frac{2}{a}<x<1$时,f'(x)>0;
∴f(x)极大值为$f(1)=-\frac{a}{2}>0$,
f(x)的极小值为$f(\frac{2}{a})=-4{({\frac{1}{a}-\frac{3}{4}})^2}-\frac{3}{4}<0$,
∴f(x)的图象与x轴有三个交点;
综上知,若a=0,f(x)的图象与x轴只有一个交点;
若a<0,f(x)的图象与x轴有三个交点…(12分)
点评 本题考查了函数的单调性、极值问题,考查导数的应用以及函数的零点问题,是一道中档题.


 学业测评一课一测系列答案
学业测评一课一测系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{9}$ | B. | $\frac{2}{3}$ | C. | $-\frac{2}{3}$ | D. | $-\frac{7}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
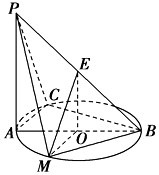 如图所示,PA⊥平面ABC,点C在以AB为直径的⊙O上,∠CBA=30°,PA=AB=2,点E为线段PB的中点,点M在$\widehat{AB}$上,且OM∥AC.
如图所示,PA⊥平面ABC,点C在以AB为直径的⊙O上,∠CBA=30°,PA=AB=2,点E为线段PB的中点,点M在$\widehat{AB}$上,且OM∥AC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | z的实部为-$\frac{1}{2}$ | B. | z的虚部为-$\frac{1}{2}$i | ||
| C. | |z|=$\frac{1}{2}$ | D. | z的共轭复数为$\frac{1}{2}$+$\frac{1}{2}$i |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com