
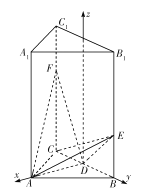
【题目】如图,在直三棱柱![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的等边三角形,
的等边三角形, ![]() 为
为![]() 的中点,侧棱
的中点,侧棱![]() ,点
,点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,且
上,且![]() ,
, ![]() .
.

(1)证明:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析(2) ![]()
【解析】试题分析:(1)根据平几知识得![]() ,由线面垂直得
,由线面垂直得![]() ,最后根据线面垂直判定定理以及面面垂直判定定理得结论,(2)先根据条件建立空间直角坐标系,设立各点坐标,根据方程组解各面法向量,根据向量数量积求向量夹角,最后根据二面角与向量夹角相等或互补关系确定二面角
,最后根据线面垂直判定定理以及面面垂直判定定理得结论,(2)先根据条件建立空间直角坐标系,设立各点坐标,根据方程组解各面法向量,根据向量数量积求向量夹角,最后根据二面角与向量夹角相等或互补关系确定二面角![]() 的余弦值.
的余弦值.
试题解析:(1)∵![]() 是等边三角形,
是等边三角形, ![]() 为
为![]() 的中点,
的中点,
∴![]() ,∴
,∴![]() 平面
平面![]() ,得
,得![]() .①
.①
在侧面![]() 中,
中,
![]() ,
, ![]() ,
,
∴![]() ,
, ![]()
∴![]() ,∴
,∴![]() .②
.②
结合①②,又∵![]() ,∴
,∴![]() 平面
平面![]() ,
,
又∵![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]()
(2)解法一:如图建立空间直角坐标系![]() .
.
则![]() ,
, ![]() ,
, ![]() .
.
得![]() ,
, ![]() ,
, ![]()
设平面![]() 的法向量
的法向量![]() ,则
,则![]()
即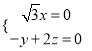 得
得![]() 取
取![]() .
.
同理可得,平面![]() 的法向量
的法向量![]()
∴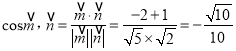
则二面角![]() 的余弦值为
的余弦值为![]() .
.
解法二:由(1)知![]() 平面
平面![]() ,∴
,∴![]() ,
, ![]() .
.
∴![]() 即二面角
即二面角![]() 的平面角
的平面角
在平面![]() 中,易知
中,易知![]() ,∴
,∴![]() ,
,
设![]() ,∵
,∵![]()
∴![]() ,解得
,解得![]() .
.
即![]() ,∴
,∴![]()
则二面角![]() 的余弦值为
的余弦值为![]() .
.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:高中数学 来源: 题型:
【题目】甲、乙二人用4张扑克牌![]() 分别是红桃2,红桃3,红桃4,方片4玩游戏,他们将扑克牌洗匀后,背面朝上放在桌面上,甲先抽,乙后抽,抽出的牌不放回,各抽一张.
分别是红桃2,红桃3,红桃4,方片4玩游戏,他们将扑克牌洗匀后,背面朝上放在桌面上,甲先抽,乙后抽,抽出的牌不放回,各抽一张.
![]() 写出甲、乙二人抽到的牌的所有情况;
写出甲、乙二人抽到的牌的所有情况;
![]() 甲乙约定,若甲抽到的牌的牌面数字比乙大,则甲胜;否则乙胜,你认为此约定是否公平?请说明理由.
甲乙约定,若甲抽到的牌的牌面数字比乙大,则甲胜;否则乙胜,你认为此约定是否公平?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .
.
(Ⅰ)求椭圆![]() 的方程.
的方程.
(Ⅱ)若![]() ,
, ![]() 是椭圆
是椭圆![]() 上两个不同的动点,且使
上两个不同的动点,且使![]() 的角平分线垂直于
的角平分线垂直于![]() 轴,试判断直线
轴,试判断直线![]() 的斜率是否为定值?若是,求出该值;若不是,说明理由.
的斜率是否为定值?若是,求出该值;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() :
:![]() 和点
和点![]() ,动圆
,动圆![]() 经过点
经过点![]() 且与圆
且与圆![]() 相切,圆心
相切,圆心![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(Ⅰ)求曲线![]() 的方程;
的方程;
(Ⅱ)四边形![]() 的顶点在曲线
的顶点在曲线![]() 上,且对角线
上,且对角线![]() 均过坐标原点,若
均过坐标原点,若![]() .
.
(i) 求![]() 的范围;(ii) 求四边形
的范围;(ii) 求四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司计划在办公大厅建一面长为![]() 米的玻璃幕墙.先等距安装
米的玻璃幕墙.先等距安装![]() 根立柱,然后在相邻的立柱之间安装一块与立柱等高的同种规格的玻璃.一根立柱的造价为6400元,一块长为
根立柱,然后在相邻的立柱之间安装一块与立柱等高的同种规格的玻璃.一根立柱的造价为6400元,一块长为![]() 米的玻璃造价为
米的玻璃造价为![]() 元.假设所有立柱的粗细都忽略不计,且不考虑其他因素,记总造价为
元.假设所有立柱的粗细都忽略不计,且不考虑其他因素,记总造价为![]() 元(总造价=立柱造价+玻璃造价).
元(总造价=立柱造价+玻璃造价).
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)当![]() 时,怎样设计能使总造价最低?
时,怎样设计能使总造价最低?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 的一段图象如图所示
的一段图象如图所示

(1)求![]() 的解析式;
的解析式;
(2)求![]() 的单调增区间,并指出
的单调增区间,并指出![]() 的最大值及取到最大值时
的最大值及取到最大值时![]() 的集合;
的集合;
(3)把![]() 的图象向左至少平移多少个单位,才能使得到的图象对应的函数为偶函数.
的图象向左至少平移多少个单位,才能使得到的图象对应的函数为偶函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个结论中正确的个数是
(1)对于命题![]() 使得
使得![]() ,则
,则![]() 都有
都有![]() ;
;
(2)已知![]() ,则
,则 ![]()
(3)已知回归直线的斜率的估计值是2,样本点的中心为(4,5),则回归直线方程为![]() ;
;
(4)“![]() ”是“
”是“![]() ”的充分不必要条件.
”的充分不必要条件.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com