
【题目】对于n∈N* , 若数列{xn}满足xn+1﹣xn>1,则称这个数列为“K数列”.
(Ⅰ)已知数列:1,m+1,m2是“K数列”,求实数m的取值范围;
(Ⅱ)是否存在首项为﹣1的等差数列{an}为“K数列”,且其前n项和Sn满足 ![]() ?若存在,求出{an}的通项公式;若不存在,请说明理由;
?若存在,求出{an}的通项公式;若不存在,请说明理由;
(Ⅲ)已知各项均为正整数的等比数列{an}是“K数列”,数列 ![]() 不是“K数列”,若
不是“K数列”,若 ![]() ,试判断数列{bn}是否为“K数列”,并说明理由.
,试判断数列{bn}是否为“K数列”,并说明理由.
【答案】解:(Ⅰ)由题意得(m+1)﹣1>1,①m2﹣(m+1)>1,②
解①得 m>1;
解②得 m<﹣1或m>2.
所以m>2,故实数m的取值范围是m>2.
(Ⅱ)假设存在等差数列{an}符合要求,设公差为d,则d>1,
由 a1=﹣1,得 ![]() ,.
,.
由题意,得 ![]() 对n∈N*均成立,
对n∈N*均成立,
即(n﹣1)d<n.
①当n=1时,d∈R;
②当n>1时, ![]() ,
,
因为 ![]() ,
,
所以d≤1,与d>1矛盾,
故这样的等差数列{an}不存在.
(Ⅲ)设数列{an}的公比为q,则 ![]() ,
,
因为{an}的每一项均为正整数,且an+1﹣an=anq﹣an=an(q﹣1)>1>0,
所以a1>0,且q>1.
因为an+1﹣an=q(an﹣an﹣1)>an﹣an﹣1 ,
所以在{an﹣an﹣1}中,“a2﹣a1”为最小项.
同理,在 ![]() 中,“
中,“ ![]() ”为最小项.
”为最小项.
由{an}为“K数列”,只需a2﹣a1>1,即 a1(q﹣1)>1,
又因为 ![]() 不是“K数列”,且“
不是“K数列”,且“ ![]() ”为最小项,所以
”为最小项,所以 ![]() ,即 a1(q﹣1)≤2,
,即 a1(q﹣1)≤2,
由数列{an}的每一项均为正整数,可得 a1(q﹣1)=2,
所以a1=1,q=3或a1=2,q=2.
①当a1=1,q=3时, ![]() ,则
,则 ![]() ,
,
令 ![]() ,则
,则 ![]() ,
,
又 ![]() =
= ![]() ,
,
所以{cn}为递增数列,即 cn>cn﹣1>cn﹣2>…>c1 ,
所以bn+1﹣bn>bn﹣bn﹣1>bn﹣1﹣bn﹣2>…>b2﹣b1 .
因为 ![]() ,
,
所以对任意的n∈N* , 都有bn+1﹣bn>1,
即数列{cn}为“K数列”.
②当a1=2,q=2时, ![]() ,则
,则 ![]() .因为
.因为 ![]() ,
,
所以数列{bn}不是“K数列”.
综上:当 ![]() 时,数列{bn}为“K数列”,
时,数列{bn}为“K数列”,
当 ![]() 时,数列{bn}不是“K数列”
时,数列{bn}不是“K数列”
【解析】(Ⅰ)由题意得(m+1)﹣1>1,m2﹣(m+1)>1,联立解出即可得出.(Ⅱ)假设存在等差数列{an}符合要求,设公差为d,则d>1,由题意,得 ![]() 对n∈N*均成立,化为(n﹣1)d<n.对n分类讨论解出即可得出.(Ⅲ)设数列{an}的公比为q,则
对n∈N*均成立,化为(n﹣1)d<n.对n分类讨论解出即可得出.(Ⅲ)设数列{an}的公比为q,则 ![]() ,由题意可得:{an}的每一项均为正整数,且an+1﹣an=anq﹣an=an(q﹣1)>1>0,可得a1>0,且q>1.由an+1﹣an=q(an﹣an﹣1)>an﹣an﹣1 , 可得在{an﹣an﹣1}中,“a2﹣a1”为最小项.同理,在
,由题意可得:{an}的每一项均为正整数,且an+1﹣an=anq﹣an=an(q﹣1)>1>0,可得a1>0,且q>1.由an+1﹣an=q(an﹣an﹣1)>an﹣an﹣1 , 可得在{an﹣an﹣1}中,“a2﹣a1”为最小项.同理,在 ![]() 中,“
中,“ ![]() ”为最小项.再利用“K数列”,可得a1=1,q=3或a1=2,q=2.进而得出.
”为最小项.再利用“K数列”,可得a1=1,q=3或a1=2,q=2.进而得出.


科目:高中数学 来源: 题型:
【题目】对于函数![]() ,若
,若![]() ,则称
,则称![]() 为
为![]() 的“不动点”;若
的“不动点”;若![]() ,则称
,则称![]() 为
为![]() 的“稳定点”.函数
的“稳定点”.函数![]() 的“不动点”和“稳定点”的集合分别记为
的“不动点”和“稳定点”的集合分别记为![]() 和
和![]() ,即
,即![]() ,
,![]() .
.
(![]() )设函数
)设函数![]() ,求集合
,求集合![]() 和
和![]() .
.
(![]() )求证:
)求证:![]() .
.
(![]() )设函数
)设函数![]() ,且
,且![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,平面五边形ABCDE中,AB∥CD,∠BAD=90°,AB=2,CD=1,△ADE是边长为2的正三角形.现将△ADE沿AD折起,得到四棱锥E﹣ABCD(如图2),且DE⊥AB.
(Ⅰ)求证:平面ADE⊥平面ABCD;
(Ⅱ)求平面BCE和平面ADE所成锐二面角的大小;
(Ⅲ)在棱AE上是否存在点F,使得DF∥平面BCE?若存在,求 ![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.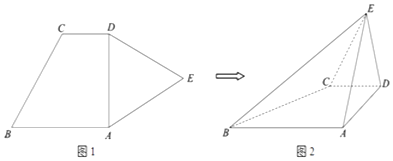
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,求
时,求![]() 的值域;
的值域;
(2)当![]() 时,函数
时,函数![]() 的图象关于
的图象关于![]() 对称,求函数
对称,求函数![]() 的对称轴.
的对称轴.
(3)若![]() 图象上有一个最低点
图象上有一个最低点![]() ,如果图象上每点纵坐标不变,横坐标缩短到原来的
,如果图象上每点纵坐标不变,横坐标缩短到原来的![]() 倍,然后向左平移1个单位可得
倍,然后向左平移1个单位可得![]() 的图象,又知
的图象,又知![]() 的所有正根从小到大依次为
的所有正根从小到大依次为![]() ,且
,且![]() ,求
,求![]() 的解析式.
的解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解春季昼夜温差大小与某种子发芽多少之间的关系,现在从4月份的30天中随机挑选了5天进行研究,且分别记录了每天昼夜温差与每天每100颗种子浸泡后的发芽数,得到如下表格:
日期 | 4月1日 | 4月7日 | 4月15日 | 4月21日 | 4月30日 |
温差x/℃ | 10 | 11 | 13 | 12 | 8 |
发芽数y/颗 | 23 | 25 | 30 | 26 | 16 |
(1)从这5天中任选2天,记发芽的种子数分别为![]() ,求事件“
,求事件“![]() 均不小于25”的概率;
均不小于25”的概率;
(2) 若由线性回归方程得到的估计数据与4月份所选5天的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的. 请根据4月7日,4月15日与4月21日这三天的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并判定所得的线性回归方程是否可靠?
,并判定所得的线性回归方程是否可靠?
参考公式:  ,
, ![]()
参考数据: ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知各项均为正数的数列![]() 的首项
的首项![]() ,
, ![]() 是数列
是数列![]() 的前
的前![]() 项和,且满足:
项和,且满足:
![]() .
.
(1)若![]() 成等比数列,求实数
成等比数列,求实数![]() 的值;
的值;
(2)若![]() ,求证:数列
,求证:数列 为等差数列;
为等差数列;
(3)在(2)的条件下,求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com