练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    （09年淄博一模）（12分）

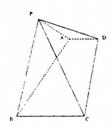
    如图，已知里棱锥的底面为直角梯形，

    （1）证明平面平面ABCD；

    （2）如果，且侧面的面积为8，求四棱锥的面积。

    解析：（Ⅰ）取AB、CD 的中点E、F。连结PE、EF、PF，由PA=PB、PC=PD

    得

    EF为直角梯形的中位线，

    又平面

    平面,得

    又且梯形两腰AB、CD必交

    （Ⅱ）方法一：由（Ⅰ）及二面角的定义知，为二面角P-CD-A的平面角等于600

    作于，连

    故为二面角P-BC-A的平面角

    由已知，得

    于是

    即二面角P-BC-A等于600

    方法二：作，由于PE、EF、EG两两垂直，建立如图所示的空间直角坐标系

    由（Ⅰ）及二面角的定义知为二面角的平面角等于600

    设平面PBC的法向量为

    又平面ABCD的法向量为

    二面角P-BC-A的大小为600

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （09年淄博一模文）(14分)

    如图，在中，，一曲线E过点C，动点P在曲线E上运动，并保持的值不变，直线l经过点A与曲线E交于两点。

    （1）建立适当的坐标系，求取现E的方程；

    （2）设直线l的斜率为k，若为钝角，求k的取值范围。

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （09年淄博一模）为了解某校高三学生的视力情况，随机地抽查了该校1000名高三学生的视力情况，得到频率分布直方图，如图，由于不慎将部分数据丢失，但知道前4组的频数成等比数列，后6组的频数成等差数列，设最大频率为，视力在4.6到5.0之间的学生数b，则的值分别为

    A ．2.7，780         B．2.7，830        C ．0.27，780         D ．0.27，830

    查看答案和解析>>

    同步练习册答案