【题目】如图是2018年第一季度五省GDP情况图，则下列陈述中不正确的是
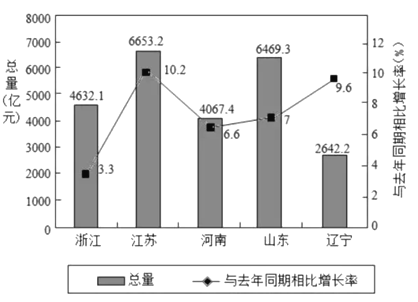
A. 2018年第一季度GDP增速由高到低排位第5的是浙江省
B. 与2017年同期相比，各省2018年第一季度的GDP总量实现了增长
C. 2017年同期河南省的GDP总量不超过4000亿元
D. 2018年第一季度GDP总量和增速由高到低排位均居同一位的省只有1个
【答案】D
【解析】
解决本题需要从统计图获取信息，由此关键是明确图表中数据的来源以及所表示的意义，依据所示的实际意义获取正确的信息。
对于A，从折线统计图可得，2018年第一季度GDP增速由高到低排位依次为江苏、辽宁、山东、河南、浙江，故浙江省排在第五，
对于B，从折线统计图可得，与2017年同期相比，各省2018年第一季度的GDP总量实现了增长率都为正值，所以与2017年同期相比，各省2018年第一季度的GDP总量实现了增长，
对于C，根据统计图可计算2017年同期河南省的GDP总量为
，所以2017年同期河南省的GDP总量不超过4000亿元，
对于D, 2018年第一季度GDP总量和增速由高到低排位均居同一位的省有两个，江苏、河南，
综述只有D选项不正确，
故答案选D
科目：高中数学 来源： 题型：
【题目】《朗读者》是一档文化情感类节目，以个人成长、情感体验、背景故事与传世佳作相结合的方式，选用精美的文字，用最平实的情感读出文字背后的价值，深受人们的喜爱.为了了解人们对该节目的喜爱程度，某调查机构随机调查了
，
两个城市各100名观众，得到下面的列联表.
非常喜爱 | 喜爱 | 合计 | |
| 60 | 100 | |
| 30 | ||
合计 | 200 |
完成上表，并根据以上数据，判断是否有
的把握认为观众的喜爱程度与所处的城市有关？
附参考公式和数据：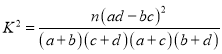
（其中
）.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
，其中
是自然对数的底数，
.
(1) 若
是函数
的导函数，当
时，解关于
的不等式
；
(2) 若在
上是单调增函数，求
的取值范围；
(3) 当
时，求整数
的所有值，使方程
在
上有解．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知f（x）=ax2+bx+c（a≠0），满足条件f（x+1）-f（x）=2x（x∈R），且f（0）=1．
（Ⅰ）求f（x）的解析式；
（Ⅱ）当x≥0时，f（x）≥mx-3恒成立，求实数m的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某单位有员工1000名，平均每人每年创造利润10万元．为增加企业竞争力，决定优化产业结构，调整出
名员工从事第三产业，调整后平均每人每年创造利润为
万元
，剩下的员工平均每人每年创造的利润可以提高
．
（1）若要保证剩余员工创造的年总利润不低于原来1000名员工创造的年总利润，则最多调整出多少名员工从事第三产业？
（2）若要保证剩余员工创造的年总利润不低于原来1000名员工创造的年总利润条件下，若要求调整出的员工创造出的年总利润始终不高于剩余员工创造的年总利润，则
的取值范围是多少？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
的图象在点
处的切线为
，若函数满足
（其中
为函数的定义域，当
时，
恒成立，则称
为函数的“转折点”，已知函数
在区间
上存在一个“转折点”，则
的取值范围是
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】过椭圆E：
1（a＞b＞0）上一动点P向圆O：x2+y2＝b2引两条切线PA，PB，切点分别是A，B．直线AB分别与x轴，y轴交于点M，N（O为坐标原点）．
（1）若在椭圆E上存在点P，满足PA⊥PB，求椭圆E的离心率的取值范围；
（2）求证：在椭圆E内，存在一点C满足|CO|＝|CA|＝|CP|＝|CB|；
（3）若椭圆E的短轴长为2，△MON面积的最小值为
，求椭圆E的方程．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知抛物线方程为y2＝－4x，直线l的方程为2x＋y－4＝0，在抛物线上有一动点A，点A到y轴的距离为m，到直线l的距离为n，则m＋n的最小值为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
