
(本题满分10分)如图,已知四棱锥S-ABCD的底面ABCD是正方形,SA⊥底面ABCD,E是SC上的一点.
(1)求证:平面EBD⊥平面SAC;
(2)设SA=4,AB=2,求点A到平面SBD的距离;

 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案科目:高中数学 来源:2014届河南省高二上学期期末考试理科数学试卷(解析版) 题型:解答题
(本题满分10分)
如图,已知正四棱柱ABCD—A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,过点B作B1C的垂线交侧棱CC1于点E,交B1C于点F,

⑴求证:A1C⊥平面BDE;
⑵求A1B与平面BDE所成角的正弦值。
查看答案和解析>>
科目:高中数学 来源:2011-2012学年甘肃省高三第二次诊断性考试理科数学试卷 题型:解答题
(本题满分10分)
如图,一个圆形游戏转盘被分成6个均匀的扇形区域.用力旋转转盘,转盘停止转动时,箭头A所指区域的数字就是每次游戏所得的分数(箭头指向两个区域的边界时重新转动),且箭头A指向每个区域的可能性都是相等的.在一次家庭抽奖的活动中,要求每个家庭派一位儿童和一位成人先后分别转动一次游戏转盘,得分情况记为 (假设儿童和成人的得分互不影响,且每个家庭只能参加一次活动).
(假设儿童和成人的得分互不影响,且每个家庭只能参加一次活动).
(Ⅰ)求某个家庭得分为 的概率?
的概率?
(Ⅱ)若游戏规定:一个家庭的得分为参与游戏的两人得分之和,且得分大于等于8的家庭可以获得一份奖品.请问某个家庭获奖的概率为多少?
(Ⅲ)若共有5个家庭参加家庭抽奖活动.在(Ⅱ)的条件下,记获奖的家庭数为 ,求
,求 的分布列及数学期望.
的分布列及数学期望.

查看答案和解析>>
科目:高中数学 来源:2011年福建省龙岩市高一上学期期末考试数学试卷 题型:解答题
(本题满分10分)如图,四边形ABCD是正方形,PB^平面ABCD,MA^平面ABCD,
PB=AB=2MA. 求证:(1)平面AMD∥平面BPC;(2)平面PMD^平面PBD.

查看答案和解析>>
科目:高中数学 来源:2013届内蒙古呼伦贝尔市高二上学期第一次综合考试理科数学 题型:解答题
(本题满分10分)如图,平行四边形EFGH的四个顶点分别在空间四边形ABCD的边AB、BC、CD、DA上,求证:BD∥面EFGH.

查看答案和解析>>
科目:高中数学 来源:2011年浙江省台州中学高二上学期第一次统练试题理科数学 题型:解答题
本题满分10分)如图,在长方体 -
- 中,
中, 分别是
分别是 ,
,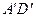 的中点,
的中点, 分别是
分别是 ,
,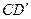 中点,
中点,

(Ⅰ)求三棱锥 的体积;
的体积;
(Ⅱ)求证:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com