
【题目】已知f(x)=ex﹣ax2﹣2x+b(e为自然对数的底数,a,b∈R)
(1)设f′(x)为f(x)的导函数,求f′(x)的递增区间;
(2)当a>0时,证明:f′(x)的最小值小于零;
(3)若a<0,f(x)>0恒成立,求符合条件的最小整数b.
【答案】
(1)解:令g(x)=f′(x)=ex﹣2ax﹣2,则g′(x)=ex﹣2a
当a≤0 时,g′(x)>0恒成立,此时f′(x)的单调递增区间是(﹣∞,+∞);
当a>0,令g′(x0)=0,解得x0=ln2a,
则当x<ln2a时,g′(x)<0,g(x)单调递减;
当x>ln2a时,g′(x)>0,g(x)单调递增;
综上所述,当a≤0时,f′(x)的单调递增区间是(﹣∞,+∞);
当a>0时,f′(x)的单调递增区间是(ln2a,+∞)
(2)证明:由(1)可知,当a>0时,x0=ln2a时,f′(x)有最小值,
则f′(x)min=g(x)min=g(ln2a)=eln2a﹣2aln2a﹣2=2a﹣2aln2a﹣2
令G(x)=x﹣xlnx﹣2(x>0),G′(x)=1﹣(1+lnx)=﹣lnx,
当x∈(0,1)时,G′(x)>0,G(x)单调递增;
当x∈(1,+∞)时,G′(x)<0,G(x)单调递减,
∴G(x)max=G(1)=﹣1<0,∴f′(x)min<0成立
(3)解:f(x)>0恒成立,等价于f(x)min>0恒成立.
令g(x)=f′(x)=ex﹣2ax﹣2,则g′(x)=ex﹣2a,
∵a<0,∴g′(x)>0,g(x)单调递增,
又g(0)=﹣1<0,g(1)=e﹣2a>0,
∴存在x0∈(0,1),使得g(x0)=0
则x<x0时,g(x)=f′(x)<0,f(x)单调递减;
x>x0时,g(x)=f′(x)>0,f(x)单调递增;
∴f(x)min=f(x0)=ex0﹣ax02﹣2x0+b>0恒成立,且ex0﹣2ax0﹣2=0
由上可知,b>﹣ex0+ax02+2x0=﹣ex0+x0( ![]() ﹣1)+2x0=(
﹣1)+2x0=( ![]() ﹣1)ex0+x0
﹣1)ex0+x0
又可得,a= ![]() <0,∴x0∈(0,ln2)
<0,∴x0∈(0,ln2)
令m(x)=( ![]() x﹣1)ex+x,x∈(0,ln2),
x﹣1)ex+x,x∈(0,ln2),
令n(x)=m′(x)= ![]() (x﹣1)ex+1,n′(x)=
(x﹣1)ex+1,n′(x)= ![]() xex>0,
xex>0,
∴n(x)>n(0)= ![]() >0,∴m(x)单调递增,m(x)>m(0)=(﹣1)e0=﹣1,
>0,∴m(x)单调递增,m(x)>m(0)=(﹣1)e0=﹣1,
m(x)<m(ln2)=( ![]() ﹣1)eln2+ln2=2ln2﹣2
﹣1)eln2+ln2=2ln2﹣2
∴b>﹣1,∴符合条件的最小整数b=0
【解析】(1)令g(x)=f′(x)=ex﹣2ax﹣2,求得g(x)导数,讨论当a≤0 时,当a>0时,由导数大于0,可得增区间;导数小于0,可得减区间;(2)f′(x)min=g(x)min=g(ln2a)=eln2a﹣2aln2a﹣2=2a﹣2aln2a﹣2,令G(x)=x﹣xlnx﹣2(x>0),求得导数和单调区间,可得G(x)的最大值,即可得证;(3)f(x)>0恒成立,等价于f(x)min>0恒成立.令g(x)=f′(x)=ex﹣2ax﹣2,求出g(x)的零点所在区间,得到f(x)的单调区间和最小值,即f(x)min=f(x0)=ex0﹣ax02﹣2x0+b>0恒成立,且ex0﹣2ax0﹣2=0,再由参数分离和构造函数法,即可得到b的范围,进而得到最小整数b.
【考点精析】解答此题的关键在于理解利用导数研究函数的单调性的相关知识,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减,以及对函数的最大(小)值与导数的理解,了解求函数
在这个区间单调递减,以及对函数的最大(小)值与导数的理解,了解求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在内的极值;(2)将函数
![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值.
比较,其中最大的是一个最大值,最小的是最小值.


科目:高中数学 来源: 题型:
【题目】“过大年,吃水饺”是我国不少地方过春节的一大习俗,2018年春节前夕,![]() 市某质检部门随机抽取了100包某种品牌的速冻水饺,检测其某项质量指标.
市某质检部门随机抽取了100包某种品牌的速冻水饺,检测其某项质量指标.
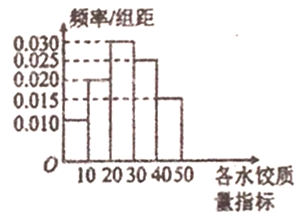
(1)求所抽取的100包速冻水饺该项质量指标值的样本平均数![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(2)①由直方图可以认为,速冻水饺的该项质量指标值![]() 服从正态分布
服从正态分布![]() ,利用该正态分布,求
,利用该正态分布,求![]() 落在
落在![]() 内的概率;
内的概率;
②将频率视为概率,若某人从某超市购买了4包这种品牌的速冻水饺,记这4包速冻水饺中这种质量指标值位于![]() 内的包数为
内的包数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:①计算得所抽查的这100包速冻水饺的质量指标的标准差为![]() ;
;
②若![]() ,则
,则![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,以
中,以![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,圆
轴正半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为 为参数),直线
为参数),直线![]() 和圆
和圆![]() 交于
交于![]() 两点,
两点,![]() 是圆
是圆![]() 上不同于
上不同于![]() 的任意一点.
的任意一点.
(1)求圆心的极坐标;
(2)求点![]() 到直线
到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学校本课程开设了A、B、C、D共4门选修课,每个学生必须且只能选修1门选修课,现有该校的甲、乙、丙3名学生:
(Ⅰ)求这3名学生选修课所有选法的总数;
(Ⅱ)求恰有2门选修课没有被这3名学生选择的概率;
(Ⅲ)求A选修课被这3名学生选择的人数![]() 的分布列 .
的分布列 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过抛物线y=![]() 焦点F的直线交抛物线于A,B两点,点C在直线y=-1上,若△ABC为正三角形,则其边长为
焦点F的直线交抛物线于A,B两点,点C在直线y=-1上,若△ABC为正三角形,则其边长为
A. 11 B. 13 C. 14 D. 12
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com