Question

【题目】如图，在四棱锥P﹣ABCD中，AD∥BC，∠ADC=∠PAB=90°，BC=CD= AD．E为棱AD的中点，异面直线PA与CD所成的角为90°．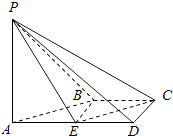

（1）在平面PAB内找一点M，使得直线CM∥平面PBE，并说明理由；
（2）若二面角P﹣CD﹣A的大小为45°，求直线PA与平面PCE所成角的正弦值．

Answer 1

【答案】
（1）解：延长AB交直线CD于点M，∵点E为AD的中点，∴AE=ED= AD，

∵BC=CD= AD，∴ED=BC，

∵AD∥BC，即ED∥BC．∴四边形BCDE为平行四边形，即EB∥CD．

∵AB∩CD=M，∴M∈CD，∴CM∥BE，

∵BE平面PBE，∴CM∥平面PBE，

∵M∈AB，AB平面PAB，

∴M∈平面PAB，故在平面PAB内可以找到一点M（M=AB∩CD），使得直线CM∥平面PBE．

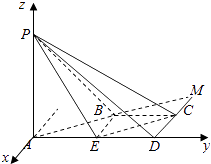
（2）解：如图所示，∵∠ADC=∠PAB=90°，异面直线PA与CD所成的角为90°，AB∩CD=M，

∴AP⊥平面ABCD．

∴CD⊥PD，PA⊥AD．

因此∠PDA是二面角P﹣CD﹣A的平面角，大小为45°．

∴PA=AD．

不妨设AD=2，则BC=CD= AD=1．∴P（0，0，2），E（0，1，0），C（﹣1，2，0），

∴ =（﹣1，1，0）， =（0，1，﹣2）， =（0，0，2），

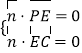设平面PCE的法向量为 =（x，y，z），则 ，可得： ．

令y=2，则x=2，z=1，∴ =（2，2，1）．

设直线PA与平面PCE所成角为θ，

则sinθ= = = = ．

【解析】（1）延长AB交直线CD于点M，由点E为AD的中点，可得AE=ED= AD，由BC=CD= AD，可得ED=BC，已知ED∥BC．可得四边形BCDE为平行四边形，即EB∥CD．利用线面平行的判定定理证明得直线CM∥平面PBE即可．（2）如图所示，由∠ADC=∠PAB=90°，异面直线PA与CD所成的角为90°AB∩CD=M，可得AP⊥平面ABCD．由CD⊥PD，PA⊥AD．因此∠PDA是二面角P﹣CD﹣A的平面角，大小为45°．PA=AD．不妨设AD=2，则BC=CD= AD=1．可得P（0，0，2），E（0，1，0），C（﹣1，2，0），利用法向量的性质、向量夹角公式、线面角计算公式即可得出．