
【题目】已知函数![]()
(1)若![]() 为曲线
为曲线![]() 的一条切线,求a的值;
的一条切线,求a的值;
(2)已知![]() ,若存在唯一的整数
,若存在唯一的整数![]() ,使得
,使得![]() ,求a的取值范围.
,求a的取值范围.
科目:高中数学 来源: 题型:
【题目】某电视台在一次对收看文艺节目和新闻节目的抽样调查中,随机抽取了100名电视观众,相关的数据如表所示:
类别 | 文艺节目 | 新闻节目 | 总计 |
20至40岁 | 40 | 18 | 58 |
大于40岁 | 15 | 27 | 42 |
总计 | 55 | 45 | 100 |
(1)由表中数据直观分析,收看新闻节目的观众是否与年龄有关?
(2)用分层抽样方法在收看新闻节目的观众中随机抽取5名,则大于40岁的观众应该抽取几名?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,某小区准备将闲置的一直角三角形(其中∠B=![]() ,AB=a,BC=
,AB=a,BC=![]() a)地块开发成公共绿地,设计时,要求绿地部分有公共绿地走道MN,且两边是两个关于走道MN对称的三角形(△AMN和△A′MN),现考虑方便和绿地最大化原则,要求M点与B点不重合,A′落在边BC上,设∠AMN=θ.
a)地块开发成公共绿地,设计时,要求绿地部分有公共绿地走道MN,且两边是两个关于走道MN对称的三角形(△AMN和△A′MN),现考虑方便和绿地最大化原则,要求M点与B点不重合,A′落在边BC上,设∠AMN=θ.
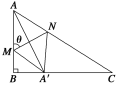
(1)若θ=![]() 时,绿地“最美”,求最美绿地的面积;
时,绿地“最美”,求最美绿地的面积;
(2)为方便小区居民的行走,设计时要求将AN,A′N的值设计最短,求此时绿地公共走道的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,某班一次数学测试成绩的茎叶图(如图甲)和频率分布直方图(如图乙)都受到不同程度的污损,其中,频率分布直方图的分组区间分别为![]() ,据此解答如下问题.(注:直方图中
,据此解答如下问题.(注:直方图中![]() 与
与![]() 对应的长方形的高度一样)
对应的长方形的高度一样)
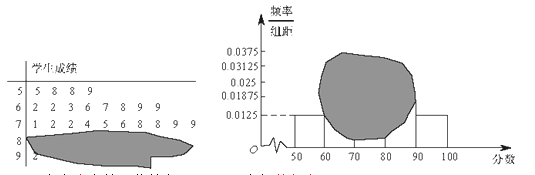
(1)若按题中的分组情况进行分层抽样,共抽取![]() 人,那么成绩在
人,那么成绩在![]() 之间应抽取多少人?
之间应抽取多少人?
(2)现从分数在![]() 之间的试卷中任取
之间的试卷中任取![]() 份分析学生失分情况,设抽取的试卷分数在
份分析学生失分情况,设抽取的试卷分数在![]() 之间 份数为
之间 份数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 与直线
与直线![]() 相切,设点
相切,设点![]() 为圆上一动点,
为圆上一动点, ![]() 轴于
轴于![]() ,且动点
,且动点![]() 满足
满足![]() ,设动点
,设动点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)直线![]() 与直线
与直线![]() 垂直且与曲线
垂直且与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com