
【题目】现安排甲、乙、丙、丁、戊5名同学参加2022年杭州亚运会志愿者服务活动,有翻译、导游、礼仪、司机四项工作可以安排,以下说法正确的是( )
A. 每人都安排一项工作的不同方法数为![]()
B. 每项工作至少有一人参加,则不同的方法数为![]()
C. 如果司机工作不安排,其余三项工作至少安排一人,则这5名同学全部被安排的不同方法数为![]()
D. 每项工作至少有一人参加,甲、乙不会开车但能从事其他三项工作,丙、丁、戊都能胜任四项工作,则不同安排方案的种数是![]()
【答案】D
【解析】
选项A中每人有四项工作可安排,5人应该是![]() ,选项A错误;选项B中先每项工作分一人,再安排另一人会有重复,选项B错误;选项C中先分组再分配中括号内的分组有重复,错误;选项D中分两类司机1人和司机2人,分类安排再相加正确.
,选项A错误;选项B中先每项工作分一人,再安排另一人会有重复,选项B错误;选项C中先分组再分配中括号内的分组有重复,错误;选项D中分两类司机1人和司机2人,分类安排再相加正确.
解:每人有四项工作可以安排,所以五人都安排一项工作的不同方法数为![]() ,选项A错误;每项工作至少有一人参加,则有一项工作安排两人,其他三项工作各一人,所以共有
,选项A错误;每项工作至少有一人参加,则有一项工作安排两人,其他三项工作各一人,所以共有![]() ,选项B中
,选项B中![]() 是先每项工作安排一人,还剩下一人在四项工作选择,这样会有重复,比如:“甲、乙、丙、丁分别安排翻译、导游、礼仪、司机,然后戊安排翻译”与“戊、乙、丙、丁分别安排翻译、导游、礼仪、司机,然后甲安排翻译”重复计算了,选项B错误;选项C中是先分组后分配,
是先每项工作安排一人,还剩下一人在四项工作选择,这样会有重复,比如:“甲、乙、丙、丁分别安排翻译、导游、礼仪、司机,然后戊安排翻译”与“戊、乙、丙、丁分别安排翻译、导游、礼仪、司机,然后甲安排翻译”重复计算了,选项B错误;选项C中是先分组后分配,![]() 代表的是5人分成3人、1人、1人三组,
代表的是5人分成3人、1人、1人三组,![]() 代表的是5人分成2人、2人、1人三组,然后三组人分配三项工作,乘以
代表的是5人分成2人、2人、1人三组,然后三组人分配三项工作,乘以![]() ,然而分组的过程中和都有重复,比如:3人、1人、1人分组中先
,然而分组的过程中和都有重复,比如:3人、1人、1人分组中先![]() 选择了甲、乙、丙三人一组,剩下丁、戊分两组只有一种分发,而不是
选择了甲、乙、丙三人一组,剩下丁、戊分两组只有一种分发,而不是![]() 种,选项C错误;选项D分两类考虑,第一类:司机安排一人为
种,选项C错误;选项D分两类考虑,第一类:司机安排一人为![]() ,另外4人分3组
,另外4人分3组![]() (4人选2人为一组,另外两人分两组只有一种分法),然后三组人安排司机除外的三项工作
(4人选2人为一组,另外两人分两组只有一种分法),然后三组人安排司机除外的三项工作![]() ,共
,共![]() ,第二类:司机安排两人
,第二类:司机安排两人![]() ,剩下3人安排另三项工作
,剩下3人安排另三项工作![]() ,共
,共![]() ,两类相加得
,两类相加得![]() ,选项D正确.
,选项D正确.
故选:D.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x(e![]() +1)
+1)
(I)求函数y=f(x)的图象在点(0,f(0))处的切线方程;
(II)若函数g(x)=f(x)-ae![]() -x,求函数g(x)在[1,2]上的最大值。
-x,求函数g(x)在[1,2]上的最大值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某居民区随机抽取10个家庭,获得第![]() 个家庭的月收入
个家庭的月收入![]() (单位:千元)与月储蓄
(单位:千元)与月储蓄![]() (单位:千元)的数据资料,算得
(单位:千元)的数据资料,算得![]() ,
, ![]() ,
,
![]() ,
, ![]()
(1).求家庭的月储蓄![]() 对月收入
对月收入![]() 的线性回归方程
的线性回归方程![]() ;
;
(2).判断变量![]() 与
与![]() 之间的正相关还是负相关;
之间的正相关还是负相关;
(3).若该居民区某家庭月收入为7千元,预测该家庭的月储蓄.
附:回归直线的斜率和截距的最小二乘估计公式分别为

![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着智能手机和电子阅读器越来越普及,人们的阅读习惯也发生了改变,手机和电子阅读产品方便易携带,越来越多的人习惯通过手机或电子阅读器阅读.某电子书阅读器厂商随机调查了![]() 人,统计了这
人,统计了这![]() 人每日平均通过手机或电子阅读器阅读的时间(单位:分钟),由统计数据得到如下频率分布直方图,已知阅读时间在
人每日平均通过手机或电子阅读器阅读的时间(单位:分钟),由统计数据得到如下频率分布直方图,已知阅读时间在![]() ,
, ![]() ,
, ![]() 三组对应的人数依次成等差数列.
三组对应的人数依次成等差数列.
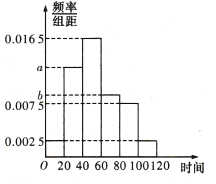
(1)求频率分布直方图中![]() ,
, ![]() 的值;
的值;
(2)若将日平均阅读时间不少于![]() 分钟的用户定义为“电子阅读发烧友”,将日平均阅读时间少于
分钟的用户定义为“电子阅读发烧友”,将日平均阅读时间少于![]() 分钟的用户定义为“电子阅读潜在爱好者”,现从上述“电子阅读发烧友”与“电子阅读潜在爱好者”的人中按分层抽样选出
分钟的用户定义为“电子阅读潜在爱好者”,现从上述“电子阅读发烧友”与“电子阅读潜在爱好者”的人中按分层抽样选出![]() 人,再从这
人,再从这![]() 人中任取
人中任取![]() 人,求恰有
人,求恰有![]() 人为“电子阅读发烧友”的概率.
人为“电子阅读发烧友”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,
中, ![]() 是坐标原点,设函数
是坐标原点,设函数![]() 的图象为直线
的图象为直线![]() ,且
,且![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,给出下列四个命题:
两点,给出下列四个命题:
①存在正实数![]() ,使
,使![]() 的面积为
的面积为![]() 的直线
的直线![]() 仅有一条;
仅有一条;
②存在正实数![]() ,使
,使![]() 的面积为
的面积为![]() 的直线
的直线![]() 仅有二条;
仅有二条;
③存在正实数![]() ,使
,使![]() 的面积为
的面积为![]() 的直线
的直线![]() 仅有三条;
仅有三条;
④存在正实数![]() ,使
,使![]() 的面积为
的面积为![]() 的直线
的直线![]() 仅有四条.
仅有四条.
其中,所有真命题的序号是( ).
A. ①②③ B. ③④ C. ②④ D. ②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确的是( )
A.若正数![]() 是等差数列,则
是等差数列,则![]() 是等比数列
是等比数列
B.若正数是![]() 等比数列,则
等比数列,则![]() 是等差数列
是等差数列
C.若正数是![]() 等差数列,则
等差数列,则![]() 是等比数列
是等比数列
D.若正数是![]() 等比数列,则是
等比数列,则是![]() 等差数列
等差数列
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com