
【题目】已知函数f(x)=2|cosx|sinx+sin2x,给出下列四个命题:
①函数f(x)的图象关于直线 ![]() 对称;
对称;
②函数f(x)在区间 ![]() 上单调递增;
上单调递增;
③函数f(x)的最小正周期为π;
④函数f(x)的值域为[﹣2,2].
其中真命题的序号是 . (将你认为真命题的序号都填上)
【答案】②④
【解析】解:对于函数f(x)=2|cosx|sinx+sin2x,由于f(﹣ ![]() )=﹣2,f(
)=﹣2,f( ![]() )=0,∴f(﹣
)=0,∴f(﹣ ![]() )≠f(
)≠f( ![]() ),
),
故f(x)的图象不关于直线 ![]() 对称,故排除①.
对称,故排除①.
在区间 ![]() 上,2x∈[﹣
上,2x∈[﹣ ![]() ,
, ![]() ],f(x)=2|cosx|sinx+sin2x=2sin2x 单调递增,故②正确.
],f(x)=2|cosx|sinx+sin2x=2sin2x 单调递增,故②正确.
函数f( ![]() )=
)= ![]() ,f(
,f( ![]() )=0,∴f(
)=0,∴f( ![]() )≠f(
)≠f( ![]() ),故函数f(x)的最小正周期不是π,故③错误.
),故函数f(x)的最小正周期不是π,故③错误.
当cosx≥0时,f(x)=2|cosx|sinx+sin2x=2sinxcosx+sin2x=2sin2x,故它的最大值为2,最小值为﹣2;
当cosx<0时,f(x)=2|cosx|sinx+sin2x=﹣2sinxcosx+sin2x=0,
综合可得,函数f(x)的最大值为2,最小值为﹣2,故④正确,
所以答案是:②④.


科目:高中数学 来源: 题型:
【题目】选修4-5:不等式选讲
已知定义在R上的函数f(x)=|x﹣m|+|x|,m∈N* , 存在实数x使f(x)<2成立.
(Ⅰ)求实数m的值;
(Ⅱ)若α,β>1,f(α)+f(β)=2,求证: ![]() +
+ ![]() ≥
≥ ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学名著《数书九章》中有“天池盆测雨”题:在下雨时,用一个圆台形的天池盆接雨水.天池盆盆口直径为二尺八寸,盆底直径为一尺二寸,盆深一尺八寸.若盆中积水深九寸,则平地降雨量是( )
(注:①平地降雨量等于盆中积水体积除以盆口面积;②一尺等于十寸;③台体的体积公式V= ![]()
A.2寸
B.3寸
C.4寸
D.5寸
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】银川一中从高二年级学生中随机抽取40名学生作为样本,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六组:![]() 后得到如图的频率分布直方图.
后得到如图的频率分布直方图.

(1)求图中实数![]() 的值;
的值;
(2)试估计我校高二年级在这次数学考试的平均分;
(3)若从样本中数学成绩在![]() 与
与![]() 两个分数段内的学生中随机选取两名学生,求这两名学生的数学成绩之差的绝对值不大于10的概率.
两个分数段内的学生中随机选取两名学生,求这两名学生的数学成绩之差的绝对值不大于10的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某水泥厂销售工作人员根据以往该厂的销售情况,绘制了该厂日销售量的频率分布直方图,如图所示:将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立. 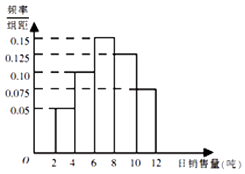
(1)求未来3天内,连续2天日销售量不低于8吨,另一天日销售量低于8吨的概率;
(2)用X表示未来3天内日销售量不低于8吨的天数,求随机变量X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设m,n为不重合的两条直线,![]() ,
,![]() 为不重合的两个平面,则下列命题中,所有真命题的个数是______.
为不重合的两个平面,则下列命题中,所有真命题的个数是______.
![]() 若
若![]() ,
,![]() ,则
,则![]() ;
;![]() 若
若![]() ,
,![]() ,则
,则![]() ;
;
![]() 若
若![]() ,
,![]() ,则
,则![]() ;
;![]() 一定存在直线l,使得
一定存在直线l,使得![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(ax2+x﹣1)ex , 其中e是自然对数的底数,a∈R.
(Ⅰ)若a=1.求曲线f(x)在点(1,f(1))处的切线方程;
(Ⅱ)若a=﹣1,函数f(x)的图象与函数g(x)=![]() x3+
x3+![]() x2+m的图象有3个不同的交点,求实数m的取值范围.
x2+m的图象有3个不同的交点,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com