
【题目】将平面上每个点染为![]() 种颜色之一,同时满足:
种颜色之一,同时满足:
(1)每种颜色的点都有无穷多个,且不全在同一条直线上;
(2)至少有一条直线上所有的点恰为两种颜色.
求![]() 的最小值,使得存在互不同色的四个点共圆.
的最小值,使得存在互不同色的四个点共圆.
【答案】5
【解析】
由已知![]() .
.
若![]() ,在平面上取一定圆
,在平面上取一定圆![]() 及上面三点
及上面三点![]() 、
、![]() 、
、![]() ,将弧
,将弧![]() (含点
(含点![]() 不含
不含![]() )、弧
)、弧![]() (含点
(含点![]() 不含
不含![]() )、弧
)、弧![]() (含点
(含点![]() 不含
不含![]() )分别染为1、2、3色,平面上其他点染为4色,则满足题意且不存在四个互不同色的点共圆.
)分别染为1、2、3色,平面上其他点染为4色,则满足题意且不存在四个互不同色的点共圆.
所以,![]() .
.
当![]() 时,假设不存在四个互不同色的点共圆.由条件(2)知,存在直线
时,假设不存在四个互不同色的点共圆.由条件(2)知,存在直线![]() 上恰有两种颜色的点(设
上恰有两种颜色的点(设![]() 上仅有颜色1、2的点),再由条件(1)知,存在颜色分别为3、4、5的点
上仅有颜色1、2的点),再由条件(1)知,存在颜色分别为3、4、5的点![]() 、
、![]() 、
、![]() 不共线,设过
不共线,设过![]() 、
、![]() 、
、![]() 的圆为
的圆为![]() (如图).
(如图).
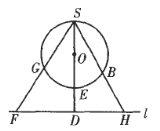
若![]() 与
与![]() 有公共点,则存在四个互不同色的点共圆,矛盾.
有公共点,则存在四个互不同色的点共圆,矛盾.
若![]() 与
与![]() 相离,则过点
相离,则过点![]() 作
作![]() 的垂线与
的垂线与![]() 交于点
交于点![]() .
.
设![]() 的颜色为1,垂线与
的颜色为1,垂线与![]() 交于点
交于点![]() 、
、![]() ,如图3.
,如图3.
设![]() 的颜色为3.考虑
的颜色为3.考虑![]() 上颜色为2的点
上颜色为2的点![]() ,
,![]() 与
与![]() 交于点
交于点![]() .
.
因为![]() ,所以,
,所以,![]() 、
、![]() 、
、![]() 、
、![]() 四点共圆.则
四点共圆.则![]() 只能为3色.
只能为3色.
又![]() 、
、![]() 必有一点不同于
必有一点不同于![]() (设为
(设为![]() ),
),![]() 与
与![]() 交于点
交于点![]() .
.
因为![]() ,所以,
,所以,![]() 、
、![]() 、
、![]() 、
、![]() 四点共圆.则
四点共圆.则![]() 只能为1色.
只能为1色.
故![]() .
.
从而,![]() 、
、![]() 、
、![]() 、
、![]() 四点共圆,且互不同色,矛盾.
四点共圆,且互不同色,矛盾.
所以,当![]() 时,存在四个互不同色的点共圆.
时,存在四个互不同色的点共圆.
因此,![]() 的最小值是5.
的最小值是5.


科目:高中数学 来源: 题型:
【题目】已知双曲线![]() :
: ![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
, ![]() 为坐标原点,
为坐标原点, ![]() 是双曲线上在第一象限内的点,直线
是双曲线上在第一象限内的点,直线![]() 分别交双曲线
分别交双曲线![]() 左、右支于另一点
左、右支于另一点![]() ,
, ![]() ,且
,且![]() ,则双曲线
,则双曲线![]() 的离心率为( )
的离心率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】农历戊戌年即将结束,为了迎接新年,小康、小梁、小谭、小刘、小林每人写了一张心愿卡,设计了一个与此心愿卡对应的漂流瓶.现每人随机的选择一个漂流瓶将心愿卡放入,则事件“至少有两张心愿卡放入对应的漂流瓶”的概率为___
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年1月10日,引发新冠肺炎疫情的![]() 病毒基因序列公布后,科学家们便开始了病毒疫苗的研究过程.但是类似这种病毒疫苗的研制需要科学的流程,不是一朝一夕能完成的,其中有一步就是做动物试验.已知一个科研团队用小白鼠做接种试验,检测接种疫苗后是否出现抗体.试验设计是:每天接种一次,3天为一个接种周期.已知小白鼠接种后当天出现抗体的概率为
病毒基因序列公布后,科学家们便开始了病毒疫苗的研究过程.但是类似这种病毒疫苗的研制需要科学的流程,不是一朝一夕能完成的,其中有一步就是做动物试验.已知一个科研团队用小白鼠做接种试验,检测接种疫苗后是否出现抗体.试验设计是:每天接种一次,3天为一个接种周期.已知小白鼠接种后当天出现抗体的概率为![]() ,假设每次接种后当天是否出现抗体与上次接种无关.
,假设每次接种后当天是否出现抗体与上次接种无关.
(1)求一个接种周期内出现抗体次数![]() 的分布列;
的分布列;
(2)已知每天接种一次花费100元,现有以下两种试验方案:
①若在一个接种周期内连续2次出现抗体即终止本周期试验,进行下一接种周期,试验持续三个接种周期,设此种试验方式的花费为![]() 元;
元;
②若在一个接种周期内出现2次或3次抗体,该周期结束后终止试验,已知试验至多持续三个接种周期,设此种试验方式的花费为![]() 元.本着节约成本的原则,选择哪种实验方案.
元.本着节约成本的原则,选择哪种实验方案.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面上有12个点且任意三点不共线.以其中任意一点为始点、另一点为终点作向量且作出所有的向量,其中,三边向量的和为零向量的三角形称为“零三角形”.求以这12个点为顶点的零三角形个数的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量![]() =(1,-3,2),
=(1,-3,2),![]() =(-2,1,1),点A(-3,-1,4),B(-2,-2,2).
=(-2,1,1),点A(-3,-1,4),B(-2,-2,2).
(1)求|2![]() +
+![]() |;
|;
(2)在直线AB上,是否存在一点E,使得![]() ⊥
⊥ ![]() ?(O为原点)
?(O为原点)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com