
分析 (1)写出直线的斜率利用判别式求最值;
(2)直线与圆相交,注意半径、弦心距、弦长的一半构成的直角三角形,确定圆C截直线l所得的弦所对的圆心角小于$\frac{2π}{3}$,即可得出结论.
解答 解:(1)直线l的方程可化为y=$\frac{m}{{m}^{2}+1}$x-$\frac{4m}{{m}^{2}+1}$,斜率k=$\frac{m}{{m}^{2}+1}$,
即km2-m+k=0,k=0时,m=0成立;
又∵△≥0,∴1-4k2≥0,
所以,斜率k的取值范围是[-$\frac{1}{2}$,$\frac{1}{2}$].
(2)不能.由(1)知l的方程为y=k(x-4),其中|k|≤$\frac{1}{2}$;
圆C的圆心为C(4,-2),半径r=2;圆心C到直线l的距离d=$\frac{2}{\sqrt{1+{k}^{2}}}$
由|k|≤$\frac{1}{2}$,得d≥$\frac{4}{\sqrt{5}}$>1,即d>$\frac{r}{2}$,
从而,若l与圆C相交,则圆C截直线l所得的弦所对的圆心角小于$\frac{2π}{3}$,
所以l不能将圆C分割成弧长的比值为1:2的两段弧.
点评 本题考查直线与圆及不等式知识的综合应用,考查点到直线的距离公式,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:解答题
| 优秀 | 非优秀 | 总计 | |
| 男生 | 40 | 20 | 60 |
| 女生 | 20 | 30 | 50 |
| 总计 | 60 | 50 | 110 |
| P(K2≥k) | 0.500 | 0.400 | 0.100 | 0.010 | 0.001 |
| k | 0.455 | 0.708 | 2.706 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{101}}{2}$ | B. | $\frac{\sqrt{97}}{2}$ | C. | $\frac{\sqrt{103}}{2}$ | D. | $\frac{\sqrt{105}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
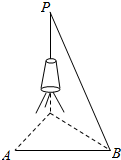 如图所示,要测量河对岸一电视塔的高PC,在河旁取A、B两点,测得AB=100$\sqrt{3}$米,∠CAB=∠ABC=60°,PB与地面所成的角为30°.
如图所示,要测量河对岸一电视塔的高PC,在河旁取A、B两点,测得AB=100$\sqrt{3}$米,∠CAB=∠ABC=60°,PB与地面所成的角为30°.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com