
【题目】已知曲线C的参数方程为![]() (
(![]() 为参数),P是曲线C上的点且对应的参数为
为参数),P是曲线C上的点且对应的参数为![]() ,
,![]() .直线l过点P且倾斜角为
.直线l过点P且倾斜角为![]() .
.
(1)求曲线C的普通方程和直线l的参数方程.
(2)已知直线l与x轴,y轴分别交于![]() ,求证:
,求证:![]() 为定值.
为定值.
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为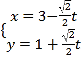 (
(![]() 为参数),在以坐标原点为极点,
为参数),在以坐标原点为极点,![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() 的方程为
的方程为![]() .
.
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设曲线![]() 与直线
与直线![]() 交于点
交于点![]() ,点
,点![]() 的坐标为(3,1),求
的坐标为(3,1),求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 对定义域内的任意
对定义域内的任意![]() ,当
,当![]() 时,总有
时,总有![]() ,则称函数
,则称函数![]() 为单调函数,例如函数
为单调函数,例如函数![]() 是单纯函数,但函数
是单纯函数,但函数![]() 不是单纯函数,下列命题:
不是单纯函数,下列命题:
①函数![]() 是单纯函数;
是单纯函数;
②当![]() 时,函数
时,函数![]() 在
在![]() 是单纯函数;
是单纯函数;
③若函数![]() 为其定义域内的单纯函数,
为其定义域内的单纯函数, ![]() ,则
,则![]()
④若函数![]() 是单纯函数且在其定义域内可导,则在其定义域内一定存在
是单纯函数且在其定义域内可导,则在其定义域内一定存在![]() 使其导数
使其导数![]() ,其中正确的命题为__________.(填上所有正确的命题序号)
,其中正确的命题为__________.(填上所有正确的命题序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图是某省从1月21日至2月24日的新冠肺炎每日新增确诊病例变化曲线图.

若该省从1月21日至2月24日的新冠肺炎每日新增确诊人数按日期顺序排列构成数列![]() ,
,![]() 的前n项和为
的前n项和为![]() ,则下列说法中正确的是( )
,则下列说法中正确的是( )
A.数列![]() 是递增数列B.数列
是递增数列B.数列![]() 是递增数列
是递增数列
C.数列![]() 的最大项是
的最大项是![]() D.数列
D.数列![]() 的最大项是
的最大项是![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
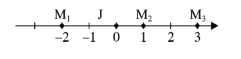
【题目】本学期开学前后,国务院下发了《新一代人工智能发展规划》,要求从小学教育,中学教育,到大学院校,逐步新增人工智能课程,建设全国人才梯队,凸显了我国抢占人工智能新高地的决心和信心.如图,三台机器人![]() 、
、![]() 、
、![]() 和检测台
和检测台![]() (位置待定)(
(位置待定)(![]() 与
与![]() 、
、![]() 、
、![]() 共线但互不重合),三台机器人需把各自生产的零件送交
共线但互不重合),三台机器人需把各自生产的零件送交![]() 处进行检测,送检程序如下:当
处进行检测,送检程序如下:当![]() 把零件送达
把零件送达![]() 处时,
处时,![]() 即刻自动出发送检;当
即刻自动出发送检;当![]() 把零件送达
把零件送达![]() 处时,
处时,![]() 即刻自动出发送检.设
即刻自动出发送检.设![]() 、
、![]() 的送检速度的大小为2,
的送检速度的大小为2,![]() 的送检速度大小为1.则三台机器人
的送检速度大小为1.则三台机器人![]() 、
、![]() 、
、![]() 送检时间之和的最小值为( ).
送检时间之和的最小值为( ).
A.8B.6C.5D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,A的坐标为(2,0),B是第一象限内的一点,以C为圆心的圆经过OAB三点,且圆C在点A,B处的切线相交于P,若P的坐标为(4,2),则直线PB的方程为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知![]() 是椭圆
是椭圆![]() 的左、右焦点,椭圆的短轴长为
的左、右焦点,椭圆的短轴长为![]() ,点
,点![]() 是椭圆
是椭圆![]() 上的一点,过点
上的一点,过点![]() 作
作![]() 轴的垂线交椭圆于另一点
轴的垂线交椭圆于另一点![]() (
(![]() 不过点
不过点![]() ),且
),且![]() 的周长的最大值为8.
的周长的最大值为8.
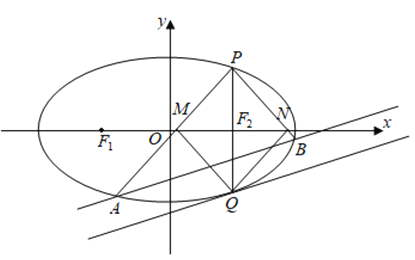
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() 过焦点
过焦点![]() ,在椭圆上取两点
,在椭圆上取两点![]() ,连接
,连接![]() ,与
,与![]() 轴的交点分别为
轴的交点分别为![]() ,过点
,过点![]() 作椭圆的切线
作椭圆的切线![]() ,当四边形
,当四边形![]() 为菱形时,证明:直线
为菱形时,证明:直线![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了解高一新生的体能情况,在入学后不久,组织了一次体能测试,按成绩分为优秀、良好、一般、较差四个档次.现随机抽取120名学生的成绩,其条形图如下:
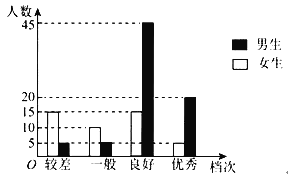
(1)将优秀、良好、一般归为合格,较差归为不合格,试根据条形图完成下面的2×2列联表,并判断能否在犯错误的概率不超过0.01的前提下认为学生的成绩与性别有关.
合格 | 不合格 | 合计 | |
男生 | |||
女生 | |||
合计 |
(2)学校为了解学生以前参加课外活动的情况,利用分层抽样的方法从120名学生中抽取24名学生参加一个座谈会.
①座谈会上抽取2名学生汇报以前参加课外活动的情况,求恰好抽到测试成绩一个优秀与一个较差的学生的概率;
②为全面提高学生的体能,学校专门安排专职教师对全校测试成绩较差的学生在课外活动时进行专项训练,通过一段时间的训陈后,测试合格率达到了![]() .若某班有4名学生参加这个专项训陈,求训练后测试合格人数ξ的分布列与数学期望.
.若某班有4名学生参加这个专项训陈,求训练后测试合格人数ξ的分布列与数学期望.
附:K2![]() ,其中n=a+b+c+d
,其中n=a+b+c+d
P(K2≥k0) | 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com