
【题目】下列说法正确的是( )
①设某大学的女生体重![]() 与身高
与身高![]() 具有线性相关关系,根据一组样本数据
具有线性相关关系,根据一组样本数据![]() ,用最小二乘法建立的线性回归方程为
,用最小二乘法建立的线性回归方程为![]() ,则若该大学某女生身高增加
,则若该大学某女生身高增加![]() ,则其体重约增加
,则其体重约增加![]() ;
;
②关于![]() 的方程
的方程![]() 的两根可分别作为椭圆和双曲线的离心率;
的两根可分别作为椭圆和双曲线的离心率;
③过定圆![]() 上一定点
上一定点![]() 作圆的动弦
作圆的动弦![]() ,
,![]() 为原点,若
为原点,若![]() ,则动点
,则动点![]() 的轨迹为椭圆;
的轨迹为椭圆;
④已知![]() 是椭圆
是椭圆![]() 的左焦点,设动点
的左焦点,设动点![]() 在椭圆上,若直线
在椭圆上,若直线![]() 的斜率大于
的斜率大于![]() ,则直线
,则直线![]() (
(![]() 为原点)的斜率的取值范围是
为原点)的斜率的取值范围是![]() .
.
A. ①②③ B. ①③④ C. ①②④ D. ②③④
【答案】C
【解析】
利用线性回归方程系数的几何意义,圆锥曲线离心率的范围,椭圆的性质,逐一判断即可.
①设某大学的女生体重y(kg)与身高x(cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的线性回归方程为![]() 0.85x﹣85.71,则若该大学某女生身高增加1cm,则其体重约增加0.85kg,正确;
0.85x﹣85.71,则若该大学某女生身高增加1cm,则其体重约增加0.85kg,正确;
②关于x的方程x2﹣mx+1=0(m>2)的两根之和大于2,两根之积等于1,故两根中,一根大于1,一根大于0小于1,故可分别作为椭圆和双曲线的离心率.正确;
③设定圆C的方程为(x﹣a)2+(x﹣b)2=r2,其上定点A(x0,y0),设B(a+rcosθ,b+rsinθ),P(x,y),
由![]() (
(![]() )得
)得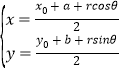 ,消掉参数θ,得:(2x﹣x0﹣a)2+(2y﹣y0﹣b)2=r2,即动点P的轨迹为圆, ∴故③不正确;
,消掉参数θ,得:(2x﹣x0﹣a)2+(2y﹣y0﹣b)2=r2,即动点P的轨迹为圆, ∴故③不正确;
④由![]() ,得a2=4,b2=3,∴
,得a2=4,b2=3,∴![]() .则F(﹣1,0),
.则F(﹣1,0),
如图:过F作垂直于x轴的直线,交椭圆于A(x轴上方),则xA=﹣1,
代入椭圆方程可得![]() .
.
当P为椭圆上顶点时,P(0,![]() ),此时
),此时![]() ,又
,又![]() ,
,
∴当直线FP的斜率大于![]() 时,直线OP的斜率的取值范围是
时,直线OP的斜率的取值范围是![]() .
.
当P为椭圆下顶点时,P(0,![]() ),
),
∴当直线FP的斜率大于![]() 时,直线OP的斜率的取值范围是(
时,直线OP的斜率的取值范围是(![]() ,
,![]() ),
),
综上,直线OP(O为原点)的斜率的取值范围是![]() ∪(
∪(![]() ,
,![]() ).
).
故选:C


科目:高中数学 来源: 题型:
【题目】了解某市今年初二年级男生的身体素质状况,从该市初二年级男生中抽取了一部分学生进行“掷实心球”的项目测试.成绩低于6米为不合格,成绩在6至8米(含6米不含8米)的为及格,成绩在8米至12米(含8米和12米,假定该市初二学生掷实心球均不超过12米)为优秀.把获得的所有数据,分成![]() 五组,画出的频率分布直方图如图所示.已知有4名学生的成绩在10米到12米之间.
五组,画出的频率分布直方图如图所示.已知有4名学生的成绩在10米到12米之间.
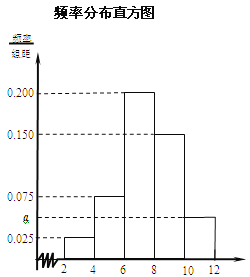
(Ⅰ)求实数![]() 的值及参加“掷实心球”项目测试的人数;
的值及参加“掷实心球”项目测试的人数;
(Ⅱ)根据此次测试成绩的结果,试估计从该市初二年级男生中任意选取一人,“掷实心球”成绩为优秀的概率;
(Ⅲ)若从此次测试成绩最好和最差的两组男生中随机抽取2 名学生再进行其它项目的测试,求所抽取的2名学生来自不同组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() (cosx,2cosx),
(cosx,2cosx),![]() (2cosx,sinx),f(x)
(2cosx,sinx),f(x)![]()
![]() .
.
(1)把f(x)的图象向右平移![]() 个单位得g(x)的图象,求g(x)的单调递增区间;
个单位得g(x)的图象,求g(x)的单调递增区间;
(2)当![]() 与
与![]() 共线时,求f(x)的值.
共线时,求f(x)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了确定下一年度投入某种产品的宣传费用,需了解年宣传费![]() (单位:万元)对年销量
(单位:万元)对年销量![]() (单位:吨)和年利润(单位:万元)的影响.对近6年宣传费
(单位:吨)和年利润(单位:万元)的影响.对近6年宣传费![]() 和年销量
和年销量![]() 的数据做了初步统计,得到如下数据:
的数据做了初步统计,得到如下数据:
年份 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年宣传费x(万元) | 38 | 48 | 58 | 68 | 78 | 88 |
年销售量y(吨) | 16.8 | 18.8 | 20.7 | 22.4 | 24.0 | 25.5 |
经电脑模拟,发现年宣传费![]() (万元)与年销售量
(万元)与年销售量![]() (吨)之间近似满足关系式
(吨)之间近似满足关系式![]() 即
即![]() ,对上述数据作了初步处理,得到相关的值如下表:
,对上述数据作了初步处理,得到相关的值如下表:
|
|
|
|
75.3 | 24.6 | 18.3 | 101.4 |
(Ⅰ)从表中所给出的6年年销售量数据中任选2年做年销售量的调研,求所选数据中至多有一年年销售量低于20吨的概率.
(Ⅱ)根据所给数据,求![]() 关于
关于![]() 的回归方程;
的回归方程;
(Ⅲ)若生产该产品的固定成本为200(万元),且每生产1(吨)产品的生产成本为20(万元)(总成本=固定成本+生产成本+年宣传费),销售收入为![]() (万元),假定该产品产销平衡(即生产的产品都能卖掉),2019年该公司计划投入
(万元),假定该产品产销平衡(即生产的产品都能卖掉),2019年该公司计划投入![]() 万元宣传费,你认为该决策合理吗?请说明理由.(其中
万元宣传费,你认为该决策合理吗?请说明理由.(其中![]() 为自然对数的底数,
为自然对数的底数,![]() )
)
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 中的斜率和截距的最小二乘估计分别为
中的斜率和截距的最小二乘估计分别为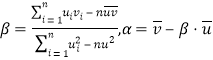 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(12分)已知函数f(x)=![]()
(1)判断函数在区间[1,+∞)上的单调性,并用定义证明你的结论.
(2)求该函数在区间[1,4]上的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2018衡水金卷(三)】如图所示,在三棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.

(I)证明: ![]() 平面
平面![]() ;
;
(II)若二面角![]() 的平面角的大小为
的平面角的大小为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“龟兔赛跑”讲述了这样的故事:领先的兔子看着慢慢爬行的乌龟,骄傲起来,睡了一觉,当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟还是先到达了终点.用![]() ,
,![]() 分别表示乌龟和兔子所行的路程,
分别表示乌龟和兔子所行的路程,![]() 为时间,则与故事情节相吻合的是( )
为时间,则与故事情节相吻合的是( )
A.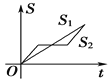 B.
B.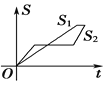 C.
C.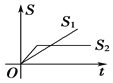 D.
D.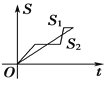
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com