
分析 由已知数列递推式求出a2,再把数列递推式变形后可得数列{an+1}从第二项起,构成以1为首项,以$\frac{3}{2}$为公比的等比数列,由等比数列的通项公式求得答案.
解答 解:由Sn=2an+1+n,①得
Sn+1=2an+2+n+1,②
②-①得an+1=2an+2-2an+1+1,
即${a}_{n+2}=\frac{3}{2}{a}_{n+1}+\frac{1}{2}$,
∴${a}_{n+2}+1=\frac{3}{2}({a}_{n+1}+1)$,
∵a1=1,∴${a}_{2}=\frac{1}{2}({a}_{1}-1)=0$,
则a2+1=1≠0.
∴数列{an+1}从第二项起,构成以1为首项,以$\frac{3}{2}$为公比的等比数列.
则当n≥2时,${a}_{n}+1=\frac{1-(\frac{3}{2})^{n-2}}{1-\frac{3}{2}}$=$2-(\frac{3}{2})^{n-2}$,
即${a}_{n}=1-(\frac{3}{2})^{n-2}$(n≥2).
验证n=1上式不成立.
∴${a_n}=\left\{{\begin{array}{l}{1(n=1)}\\{1-{{(\frac{3}{2})}^{n-2}}(n≥2)}\end{array}}\right.$.
点评 本题考查数列的递推式,考查了等比关系的确定,训练了等比数列通项公式的求法,是中档题.


科目:高中数学 来源: 题型:解答题
 某市政府欲在如图所示的矩形ABCD的非农业用地中规划出一个休闲娱乐公园(如图中阴影部分),形状为直角梯形OPRE(线段EO和RP为两条底边),已知AB=2km,BC=6km,AE=BF=4km,其中曲线AF是以A为顶点、AD为对称轴的抛物线的一部分.
某市政府欲在如图所示的矩形ABCD的非农业用地中规划出一个休闲娱乐公园(如图中阴影部分),形状为直角梯形OPRE(线段EO和RP为两条底边),已知AB=2km,BC=6km,AE=BF=4km,其中曲线AF是以A为顶点、AD为对称轴的抛物线的一部分.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
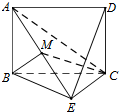 如图,已知矩形ABCD所在平面与等腰直角三角形BEC所在平面互相垂直,BE⊥EC,AB=BE,M为线段AE的中点.
如图,已知矩形ABCD所在平面与等腰直角三角形BEC所在平面互相垂直,BE⊥EC,AB=BE,M为线段AE的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=log2(x+2) | B. | y=2x-1 | C. | y=x2-$\frac{1}{2}$ | D. | y=-x3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 150° | B. | 135° | C. | 120° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,AB⊥AC,M,N分别是CC1,BC的中点,点p在直线A1B1上运动,且$\overrightarrow{{A}_{1}P}$=$λ\overrightarrow{{{A}_{1}B}_{1}}$(λ∈[0,1])
如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,AB⊥AC,M,N分别是CC1,BC的中点,点p在直线A1B1上运动,且$\overrightarrow{{A}_{1}P}$=$λ\overrightarrow{{{A}_{1}B}_{1}}$(λ∈[0,1])查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com