Question

集合A是由适合以下性质的函数f(x)构成的：

对于任意的x＞0，y＞0，且x≠y，都有f(x)＋2f(y)＞3f()．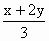

(Ⅰ)试判断f₁(x)＝log₂x及f₂(x)＝(x＋1)²是否在集合A中？说明理由；

(Ⅱ)设f(x)∈A，且定义域是(0，＋∞)，值域是(1，2)，f(1)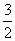＞，写出一个满足以上条件的f(x)的解析式；并证明你写出的函数f(x)∈A．

Answer 1

答案：
解析：

(Ⅰ)解：取x＝1，y＝4则 f1(1)＋2f1(4)＝log21＋2log24＝log216， 3f1()＝3log2＝log227＞log216 ∴f1(x)＋2f1(y)＜3f1 ∴f1(x)A 任取x＞0，y＞0旦x≠y，研究 f2(x)＋2f2(y)－3f2＝(x＋1)2＋2(y＋1)2－3(＋1)2 ＝(x－y)2＞0 ∴f2(x)＋2f2(y)＞3f2． ∴f2(x)∈A (Ⅱ)设函数f(x)＝()x＋1，x∈(0，＋∞)，满足其值域为(1，2) 且f(1)＝＋1＝＞ 又任意取x＞0，y＞0且x≠y则 f(x)＋2f(y)＝()x＋1＋2()y＋2＝()x＋2()y＋3 　　　　＝()x＋()y＋()y＋3＞＋3 　　　　　　　　　　　　　　　＝3[＋1] 　　　　　　　　　　　　　　　＝3f ∴f(x)∈A