
(1)1.72.5,1.73;(2)0.8-0.1,0.8-0.2;(3)1.70.3,0.93.1.
思路分析:利用单调性或中间变量.
解:(1)考查指数函数y=1.7x,由于底数1.7>1,
∴指数函数y=1.7x在(-∞,+∞)上是增函数.
∵2.5<3,∴1.72.5<1.73.
(2)考查函数y=0.8x,由于0<0.8<1,
∴指数函数y=0.8x在(-∞,+∞)上为减函数.
∵-0.1>-0.2,
∴0.8-0.1<0.8-0.2.
(3)由指数函数的性质得1.70.3>1.70=1,0.93.1<0.90=1.
∴1.70.3>0.93.1.
温馨提示
(1)对于同底数幂,要利用相应指数函数的单调性,通过自变量的大小关系可以判断相应函数值的大小.
(2)对于1.70.3与0.93.1,不能直接看成某一个指数函数的两个值.所以(3)题无法用(1)、(2)两题的方法来进行比较.本题可在这两个数值间找到数值1.使这两个数值分别与数值1进行比较,通过搭桥进而比较出1.70.3与0.93.1的大小.常插入的数值可能是0或±1.根据问题的实际也可能是其他数值.


科目:高中数学 来源:同步题 题型:解答题
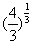 ,
,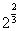 ,
, ,
,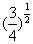 的大小。
的大小。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com