
分析 先根据条件求出题中所涉及到的角,再根据正弦定理分别求出PB,PA,即可得到结论.
解答 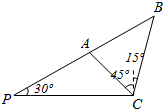 解:由题得:PC=600,∠ACP=45°,∠PAC=105°,∠PCB=105°,∠PBC=45°.
解:由题得:PC=600,∠ACP=45°,∠PAC=105°,∠PCB=105°,∠PBC=45°.
在△BCP中,$\frac{PB}{sin∠PCB}$=$\frac{PC}{sin∠PBC}$⇒PB=PC•$\frac{sin105°}{sin45°}$=300+300$\sqrt{3}$;
在△ACP中,$\frac{PC}{sin∠PAC}=\frac{PA}{sin∠PCA}$⇒PA=PC•$\frac{sin45°}{sin105°}$=600×($\sqrt{3}$-1);
∴AB=PB-PA=300+300$\sqrt{3}$-600($\sqrt{3}$-1)=900-300$\sqrt{3}$.
点评 本题主要考查解三角形的实际应用.一般解决这类问题时用正弦定理或余弦定理,本题主要涉及到正弦定理的运用以及特殊角的三角函数值.


科目:高中数学 来源: 题型:选择题
| A. | P=Q | B. | P?Q | C. | Q?P | D. | P∩Q=∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若随机事件A,B是对立事件,则A,B一定不是互斥事件 | |
| B. | 若随机事件A,B不是对立事件,则A,B一定不是互斥事件 | |
| C. | 存在随机事件A,B是对立事件,并且A,B不是互斥事件 | |
| D. | 存在随机事件A,B不是对立事件,并且A,B是互斥事件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com