
| AΘ° | 0 | BΘ° | 1 | CΘ° | 2 | DΘ° | 3 |
Ζ÷Έω άϊ”ΟΚ· ΐΒΡΤφ≈Φ–‘≈–ΕœΔΌΒΡ’ΐΈσΘΜάϊ”Ο»ΐΫ«–Έ÷–’ΐœ“Ε®άμ≈–ΕœΔΎΒΡ’ΐΈσΘ§άϊ”Ο≥δ“ΣΧθΦΰ≈–ΕœΔέΒΡ’ΐΈσΘ§ΟϋΧβΒΡΖώΕ®≈–ΕœΔήΒΡ’ΐΈσΘ°
Ϋβ¥π ΫβΘΚΕ‘”ΎΔΌΘ§»τfΘ®xΘ©=$\frac{1}{{2}^{x}+1}$+aΈΣΤφΚ· ΐΘ§‘ρfΘ®0Θ©=0Θ§ΫβΒΟa=-$\frac{1}{2}$Θ§Υυ“‘ΔΌ≤Μ’ΐ»ΖΘΜ
Ε‘”ΎΔΎΘ§ΓΑ‘ΎΓςABC÷–Θ§»τsinAΘΨsinBΘ§”…’ΐœ“Ε®άμΩ…ΒΟaΘΨbΘ§‘ρAΘΨBΓ±Θ§ΒΡΡφΟϋΧβ «’φΟϋΧβΘΜΥυ“‘ΔΎ≤Μ’ΐ»ΖΘΜ
Ε‘”ΎΔέΘ§ΓΑ»ΐΗω ΐaΘ§bΘ§c≥…Β»±» ΐΝ–Γ±‘ρb2=acΘ§Γύb=Γά$\sqrt{ac}$Θ§
»τa=b=c=0Θ§¬ζΉψb=$\sqrt{ac}$Θ§ΒΪ»ΐΗω ΐaΘ§bΘ§c≥…Β»±» ΐΝ–≤Μ≥…ΝΔΘ§
ΓύΓΑ»ΐΗω ΐaΘ§bΘ§c≥…Β»±» ΐΝ–Γ± «ΓΑb=$\sqrt{ac}$Γ±ΒΡΦ»≤Μ≥δΖ÷“≤≤Μ±Ί“ΣΧθΦΰΘ§Υυ“‘Δέ’ΐ»ΖΘ°
Ε‘”ΎΔήΘ§ΟϋΧβΓΑ?xΓ RΘ§x3-x2+1Γή0Γ±ΒΡΖώΕ® «ΓΑ?x0Γ RΘ§x03-x02+1ΘΨ0Γ±Θ°¬ζΉψΟϋΧβΒΡΖώΕ®–Έ ΫΘ§Υυ“‘Δή’ΐ»ΖΘ°
Ι ―ΓΘΚCΘ°
ΒψΤά ±ΨΧβΩΦ≤ιΟϋΧβΒΡΖώΕ®Θ§≥δ“ΣΧθΦΰΘ§ΟϋΧβΒΡ’φΦΌΒΡ≈–Εœ”κ”Π”ΟΘ§Μυ±Ψ÷Σ ΕΒΡΩΦ≤ιΘ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΧνΩ’Χβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | $Γά\frac{{\sqrt{3}}}{3}$ | BΘ° | Γά3 | CΘ° | $Γά\sqrt{2}$ | DΘ° | Γά1 |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
 »γΆΦΘ§‘Ύ±Ώ≥ΛΈΣ3ΒΡ’ΐΖΫ–ΈΡΎ”–«χ”ρAΘ®“θ”Α≤ΩΖ÷Υυ ΨΘ©Θ§’≈ΟςΆ§―ß”ΟΥφΜζΡΘΡβΒΡΖΫΖ®«σ«χ”ρAΒΡΟφΜΐΘ°»τΟΩ¥Έ‘Ύ’ΐΖΫ–ΈΡΎΟΩ¥ΈΥφΜζ≤ζ…ζ10000ΗωΒψΘ§≤ΔΦ«¬Φ¬δ‘Ύ«χ”ρAΡΎΒΡΒψΒΡΗω ΐΘ°Ψ≠ΙΐΕύ¥Έ ‘―ιΘ§ΦΤΥψ≥ω¬δ‘Ύ«χ”ρAΡΎΒψΒΡΗω ΐΤΫΨυ÷ΒΈΣ6600ΗωΘ§‘ρ«χ”ρAΒΡΟφΜΐ‘ΦΈΣΘ®ΓΓΓΓΘ©
»γΆΦΘ§‘Ύ±Ώ≥ΛΈΣ3ΒΡ’ΐΖΫ–ΈΡΎ”–«χ”ρAΘ®“θ”Α≤ΩΖ÷Υυ ΨΘ©Θ§’≈ΟςΆ§―ß”ΟΥφΜζΡΘΡβΒΡΖΫΖ®«σ«χ”ρAΒΡΟφΜΐΘ°»τΟΩ¥Έ‘Ύ’ΐΖΫ–ΈΡΎΟΩ¥ΈΥφΜζ≤ζ…ζ10000ΗωΒψΘ§≤ΔΦ«¬Φ¬δ‘Ύ«χ”ρAΡΎΒΡΒψΒΡΗω ΐΘ°Ψ≠ΙΐΕύ¥Έ ‘―ιΘ§ΦΤΥψ≥ω¬δ‘Ύ«χ”ρAΡΎΒψΒΡΗω ΐΤΫΨυ÷ΒΈΣ6600ΗωΘ§‘ρ«χ”ρAΒΡΟφΜΐ‘ΦΈΣΘ®ΓΓΓΓΘ©| AΘ° | 5 | BΘ° | 6 | CΘ° | 7 | DΘ° | 8 |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | 1-2i | BΘ° | 1+2i | CΘ° | -1-2i | DΘ° | -1+2i |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | {3Θ§5Θ§7} | BΘ° | {1Θ§5Θ§7} | CΘ° | {1Θ§3Θ§9} | DΘ° | {1Θ§2Θ§3} |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
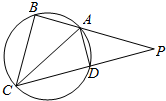 »γΆΦΘ§ΥΡ±Ώ–ΈABCD «‘≤ΡΎΫ”ΥΡ±Ώ–ΈΘ§BAΓΔCDΒΡ―”≥ΛœΏΫΜ”ΎΒψPΘ§«“AB=ADΘ§BP=2BC
»γΆΦΘ§ΥΡ±Ώ–ΈABCD «‘≤ΡΎΫ”ΥΡ±Ώ–ΈΘ§BAΓΔCDΒΡ―”≥ΛœΏΫΜ”ΎΒψPΘ§«“AB=ADΘ§BP=2BC≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com