
 中,
中, ,
, ,
, ,点
,点 、
、 分别是
分别是 、
、 的中点.
的中点.  平面
平面 ;
;  平面
平面 ;
;
 。
。 ,所以
,所以 ,然后再利用勾股定理证明
,然后再利用勾股定理证明 ,
, ,再根据面面垂直的判定定理得平面
,再根据面面垂直的判定定理得平面 平面
平面 .
.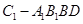 的高,然后再根据棱锥的体积计算公式计算即可.
的高,然后再根据棱锥的体积计算公式计算即可. 中,
中,
 是平行四边形.…………………1分
是平行四边形.…………………1分 , …………………2分
, …………………2分
 平面
平面 ,
, 平面
平面 ,
, 平面
平面 …………………4分
…………………4分 中,
中, ,
, ,
, ,所以
,所以 平面
平面 ,…………………6分
,…………………6分 平面
平面 ,所以
,所以
 .…………………7分
.…………………7分 中,
中, ,从而
,从而 ,
,
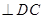 , …………………8分
, …………………8分 ,所以
,所以 平面
平面 , …………………9分
, …………………9分 平面
平面 ,所以平面
,所以平面 平面
平面 …………………10分
…………………10分 …………………14分
…………………14分

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源:不详 题型:解答题
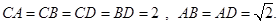
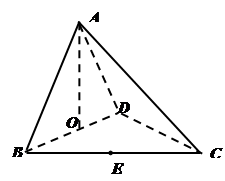
 平面BCD;
平面BCD;查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 、
、 ,直线
,直线 ,若
,若 ,
, ,则
,则 ;④四个侧面两两全等的四棱柱为直四棱柱;⑤底面是等边三角形,侧面都是等腰三角形的三棱锥是正三棱锥.其中正确命题的序号是 .
;④四个侧面两两全等的四棱柱为直四棱柱;⑤底面是等边三角形,侧面都是等腰三角形的三棱锥是正三棱锥.其中正确命题的序号是 .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com