练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】若函数为定义域上单调函数，且存在区间（其中），使得当时，的值域恰为，则称函数是上的正函数，区间叫做等域区间．如果函数是上的正函数，则实数的取值范围为 ▲ .

    【答案】

    【解析】

    解：因为函数g（x）=x2+m是（-∞，0）上的减函数，

    所以当x∈[a，b]时，

    g（a）="b" g（b）="a" 即a2+m=b，b2+m=a，

    两式相减得a2-b2=b-a，

    即b=-（a+1），

    代入a2+m=b得a2+a+m+1=0，

    由a＜b＜0，

    且b=-（a+1）

    得-1＜a＜-,

    故关于a的方程a2+a+m+1=0在区间（-1，-）内有实数解，

    记h（a）=a2+a+m+1，

    则 h（-1）＞0，h（-）＜0，

    解得m∈（-1，-）．

    故答案为（-1，-）．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】下列是合情推理的是（ ）

    ①由正三角形的性质类比出正三棱锥的有关性质；

    ②由正方形矩形的内角和是，归纳出所有四边形的内角和都是；

    ③三角形内角和是，四边形内角和是，五边形内角和是，由此得出凸边形内角和是；

    ④小李某次数学考试成绩是90分，由此推出小李的全班同学这次数学考试的成绩都是90分.

    A.①②B.①②③C.①②④D.②③④

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，三棱锥中，底面ABC，M是 BC的中点，若底面ABC是边长为2的正三角形，且PB与底面ABC所成的角为. 求：

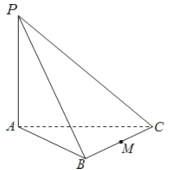
    （1）三棱锥的体积；

    （2）异面直线PM与AC所成角的大小. （结果用反三角函数值表示）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（2017-2018学年安徽省六安市第一中学高三上学期第二次月考）已知函数是偶函数.

    (1)求的值;

    (2)若函数的图象与直线没有交点,求的取值范围;

    (3)若函数,是否存在实数使得的最小值为0,若存在,求出的值;若不存在,请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的离心率为，且椭圆上一点与椭圆的两个焦点构成的三角形周长为．

    （Ⅰ）求椭圆的方程；

    （Ⅱ）设直线与椭圆交于，两点，且以为直径的圆过椭圆的右顶点，求面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】学校艺术节对同一类的，，，四项参赛作品，只评一项一等奖，在评奖揭晓前，甲、乙、丙、丁四位同学对这四项参赛作品预测如下：

    甲说：“是或作品获得一等奖”；

    乙说：“作品获得一等奖”；

    丙说：“，两项作品未获得一等奖”；

    丁说：“是作品获得一等奖”.

    若这四位同学中只有两位说的话是对的，则获得一等奖的作品是__________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，.

    （1）若，证明：；

    （2）若，有且只有个零点，求实数的取值范围；

    （3）若，，，求正整数的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】甲、乙、丙、丁、戊和己6人围坐在一张正六边形的小桌前，每边各坐一人．已知：①甲与乙正面相对；②丙与丁不相邻，也不正面相对．若己与乙不相邻，则以下选项正确的是（ ）

    A.若甲与戊相邻，则丁与己正面相对B.甲与丁相邻

    C.戊与己相邻D.若丙与戊不相邻，则丙与己相邻

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知二次函数f(x)满足f(2)＝－1，f(－1)＝－1，且f(x)的最大值是8，试确定此二次函数的解析式．

    查看答案和解析>>

    同步练习册答案