
【题目】已知平面直角坐标系xOy,在x轴的正半轴上,依次取点![]() ,
,![]() ,
,![]() ,
,![]() ,并在第一象限内的抛物线
,并在第一象限内的抛物线![]() 上依次取点
上依次取点![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,使得
,使得![]() 都为等边三角形,其中
都为等边三角形,其中![]() 为坐标原点,设第n个三角形的边长为
为坐标原点,设第n个三角形的边长为![]() .
.
⑴求![]() ,
,![]() ,并猜想
,并猜想![]() 不要求证明);
不要求证明);
⑵令![]() ,记
,记![]() 为数列
为数列![]() 中落在区间
中落在区间![]() 内的项的个数,设数列
内的项的个数,设数列![]() 的前m项和为
的前m项和为![]() ,试问是否存在实数
,试问是否存在实数![]() ,使得
,使得![]() 对任意
对任意![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的取值范围;若不存在,说明理由;
的取值范围;若不存在,说明理由;
⑶已知数列![]() 满足:
满足:![]() ,数列
,数列![]() 满足:
满足:![]() ,求证:
,求证:![]() .
.
科目:高中数学 来源: 题型:
【题目】如图所示,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E、F且EF=![]() ,则下列结论中错误的是( )
,则下列结论中错误的是( )

A.AC⊥BEB.EF![]() 平面ABCD
平面ABCD
C.三棱锥A-BEF的体积为定值D.异面直线AE,BF所成的角为定值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了鼓励学生热心公益,服务社会,成立了“慈善义工社”.2017年12月,该校“慈善义工社”为学生提供了4次参加公益活动的机会,学生可通过网路平台报名参加活动.为了解学生实际参加这4次活动的情况,该校随机抽取100名学生进行调查,数据统计如下表,其中“√”表示参加,“×”表示未参加.
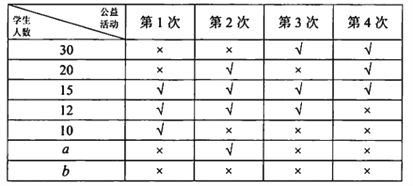
(Ⅰ)从该校所有学生中任取一人,试估计其2017年12月恰参加了2次学校组织的公益活动的概率;
(Ⅱ)若在已抽取的100名学生中,2017年12月恰参加了1次活动的学生比4次活动均未参加的学生多17人,求![]() 的值;
的值;
(Ⅲ)若学生参加每次公益活动可获得10个公益积分,试估计该校4000名学生中,2017年12月获得的公益积分不少于30分的人数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】党的十九大报告指出,建设生态文明是中华民族永续发展的千年大计.而清洁能源的广泛使用将为生态文明建设提供更有力的支撑.沼气作为取之不尽、用之不竭的生物清洁能源,在保护绿水青山方面具有独特功效.通过办沼气带来的农村“厕所革命”,对改善农村人居环境等方面,起到立竿见影的效果.为了积极响应国家推行的“厕所革命”,某农户准备建造一个深为2米,容积为32立方米的长方体沼气池,如果池底每平方米的造价为150元,池壁每平方米的造价为120元,沼气池盖子的造价为3000元,问怎样设计沼气池能使总造价最低?最低总造价是多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某服装厂每天的固定成本是30000元,每天最大规模的生产量是![]() 件.每生产一件服装,成本增加100元,生产
件.每生产一件服装,成本增加100元,生产![]() 件服装的收入函数是
件服装的收入函数是![]() ,记
,记![]() ,
,![]() 分别为每天生产
分别为每天生产![]() 件服装的利润和平均利润(
件服装的利润和平均利润(![]() ).
).
(1)当![]() 时,每天生产量
时,每天生产量![]() 为多少时,利润
为多少时,利润![]() 有最大值;
有最大值;
(2)每天生产量![]() 为多少时,平均利润
为多少时,平均利润![]() 有最大值,并求
有最大值,并求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,过抛物线上一点
,过抛物线上一点![]() 作抛物线
作抛物线![]() 的切线
的切线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,当
,当![]() 时,
时,![]() .
.
(1)判断![]() 的形状,并求抛物线
的形状,并求抛物线![]() 的方程;
的方程;
(2)若![]() 两点在抛物线
两点在抛物线![]() 上,且满足
上,且满足![]() ,其中点
,其中点![]() ,若抛物线
,若抛物线![]() 上存在异于
上存在异于![]() 的点
的点![]() ,使得经过
,使得经过![]() 三点的圆和抛物线在点
三点的圆和抛物线在点![]() 处有相同的切线,求点
处有相同的切线,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题14分)下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量(![]() 吨)与相应的生产能耗
吨)与相应的生产能耗![]() (吨)标准煤的几组对照数据:
(吨)标准煤的几组对照数据:
| 3 | 4 | 5 | 6 |
| 2.5 | 3 | 4 | 4.5 |
(1)请画出上表数据的散点图;并指出x,y 是否线性相关;
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)已知该厂技术改造前100吨甲产品能耗为90吨标准煤,试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技术改造前降低多少吨标准煤?
(参考:用最小二乘法求线性回归方程系数公式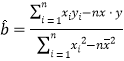 ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com