
【题目】已知函数![]() ,
, ![]() ,若曲线
,若曲线![]() 和曲线
和曲线![]() 在
在![]() 处的切线都垂直于直线
处的切线都垂直于直线![]() .
.
(Ⅰ)求![]() ,
, ![]() 的值.
的值.
(Ⅱ)若![]() 时,
时, ![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() ,
, ![]() (Ⅱ)
(Ⅱ)![]() 的取值范围是
的取值范围是![]() .
.
【解析】试题分析:
(Ⅰ)根据导数的几何意义求解即可。(Ⅱ)由(Ⅰ)设![]() ,则
,则![]() ,故只需证
,故只需证![]() 即可。由题意得
即可。由题意得![]() ,即
,即![]() ,又由
,又由![]() ,得
,得![]() ,
, ![]() ,分
,分![]() ,
, ![]() ,
, ![]() 三种情况分别讨论判断
三种情况分别讨论判断![]() 是否恒成立即可得到结论。
是否恒成立即可得到结论。
试题解析:
(I)∵![]() ,
, ![]()
∴![]() ,
, ![]() ,
,
由题意得 ![]() ,
, ![]() ,
,
解得![]() ,
, ![]() .
.
∴ ![]() ,
, ![]() .
.
(II)由(I)知![]() ,
, ![]() ,
,
设![]() ,
,
则![]() ,
,
由题设可得![]() ,即
,即![]() ,
,
令![]() ,得
,得![]() ,
, ![]() .
.
(i)若![]() ,则
,则![]() ,
,
从而当![]() 时,
时, ![]() ,
, ![]() 单调递减,
单调递减,
当![]() 时,
时, ![]() ,
, ![]() 单调递增,
单调递增,
故![]() 在
在![]() 的最小值为
的最小值为![]() ,
,
而![]() ,
,
故当![]() 时,
时, ![]() ,即
,即![]() 恒成立.
恒成立.
(ii)若![]() ,
,
则![]() ,
,
从而当![]() 时,
时, ![]() ,即
,即![]() 在
在![]() 单调递增,
单调递增,
而![]() ,
,
故当![]() 时,
时, ![]() ,即
,即![]() 恒成立.
恒成立.
(iii)若![]() ,
, ![]() ,
,
则![]() 在
在![]() 上单调递增,
上单调递增,
而![]() ,
,
从而当![]() 时,
时, ![]() 不可能恒成立,
不可能恒成立,
综上可得![]() 的取值范围是
的取值范围是![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某工厂在政府的帮扶下,准备转型生产一种特殊机器,生产需要投入固定成本![]() 万元,生产与销售均已百台计数,且每生产
万元,生产与销售均已百台计数,且每生产![]() 台,还需增加可变成本
台,还需增加可变成本![]() 万元,若市场对该产品的年需求量为
万元,若市场对该产品的年需求量为![]() 台,每生产
台,每生产![]() 百台的实际销售收入近似满足函数
百台的实际销售收入近似满足函数![]() .
.
(![]() )试写出第一年的销售利润
)试写出第一年的销售利润![]() (万元)关于年产量
(万元)关于年产量![]() (单位:百台,
(单位:百台,![]() ,
,![]() )的函数关系式:(说明:销售利润=实际销售收入-成本)
)的函数关系式:(说明:销售利润=实际销售收入-成本)
(![]() )因技术等原因,第一年的年生产量不能超过
)因技术等原因,第一年的年生产量不能超过![]() 台,若第一年的年支出费用
台,若第一年的年支出费用![]() (万元)与年产量
(万元)与年产量![]() (百台)的关系满足
(百台)的关系满足![]() ,问年产量
,问年产量![]() 为多少百台时,工厂所得纯利润最大?
为多少百台时,工厂所得纯利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P﹣ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D,E分别为AB,AC中点.
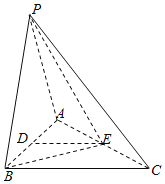
(1)求证:DE∥平面PBC;
(2)求证:AB⊥PE;
(3)求三棱锥P﹣BEC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某校参加高二年级学业水平考试模拟考试的学生中抽取60名学生,将其数学成绩分成6段[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]后,画出如图的频率分布直方图.根据图形信息,解答下列问题:
(1)估计这次考试成绩的众数,中位数,平均数;
(2)估计这次考试成绩的及格率(60分及其以上为及格).

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国在超级计算机方面发展迅速,跻身国际先进水平国家,预报天气的准确度也大大提高,天气预报说今后的三天中,每一天下雨的概率都是![]() ,我们可以通过随机模拟的方法估计概率.我们先产生
,我们可以通过随机模拟的方法估计概率.我们先产生![]() 组随机数
组随机数
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
在这组数中,用![]() 表示下雨,
表示下雨,![]() 表示不下雨,那么今后的三天中都下雨的概率近似为( )
表示不下雨,那么今后的三天中都下雨的概率近似为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】网购已经成为一种时尚,商家为了鼓励消费,购买时在店铺领取优惠券,买后给予好评返还现金等促销手段.经统计,近五年某店铺用于促销的费用![]() (万元)与当年度该店铺的销售收人
(万元)与当年度该店铺的销售收人![]() (万元)的数据如下表:
(万元)的数据如下表:
年份 | 2013年 | 2014年 | 2015年 | 2016年 | 2017年 |
促销费用 |
|
|
|
|
|
销售收入 |
|
|
|
|
|
(1)请根据上表提供的数据,用最小二乘法求出/span>![]() 关于
关于![]() 的线性回归方
的线性回归方![]() ;
;
(2)2018年度该店铺预测销售收人至少达到![]() 万元,则该店铺至少准备投入多少万元的促销费?
万元,则该店铺至少准备投入多少万元的促销费?
参考公式: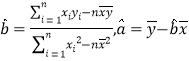
参考数据: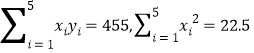
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个几何体,它的下面是一个圆柱,上面是一个圆锥,并且圆锥的底面与圆柱的上底面重合,圆柱的底面直径为3 cm,高为4 cm,圆锥的高为3 cm,画出此几何体的直观图.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com