练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    6．方程lgx+x=0的根所在的区间是（　　）
    A．$（0，\frac{1}{4}）$B．$（\frac{1}{4}，\frac{1}{2}）$C．$（\frac{1}{2}，\frac{3}{4}）$D．$（\frac{3}{4}，1）$

    分析 先确定函数为单调函数，再用零点判定定理判断即可得出结论．

    解答 解：构建函数f（x）=lgx+x，函数的定义域为（0，+∞）
    易知道函数在（0，+∞）上为单调增函数
    ∵f（$\frac{1}{4}$）=lg$\frac{1}{4}$+$\frac{1}{4}$＜0，f（$\frac{1}{2}$）=lg$\frac{1}{2}$+$\frac{1}{2}$=-lg2+lg$\sqrt{5}$=lg$\frac{\sqrt{5}}{2}$＞lg1=0，
    ∴方程lgx+x=0的根所在区间是（$\frac{1}{4}$，$\frac{1}{2}$）．
    故选：B．

    点评 本题考查方程解与函数零点之间的关系，考查零点判定定理的运用，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

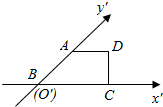    16．有一块多边形的菜地，它的水平放置的平面图形的斜二测直观图是直角梯形（如图）∠ABC=45°，AB=$\sqrt{2}$，AD=1，DC⊥BC，则这块菜地的面积为$3\sqrt{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．已知cos（$\frac{π}{3}$+α）=-$\frac{5}{13}$，且π＜α＜$\frac{3π}{2}$，则sin（$\frac{π}{6}$+$\frac{α}{2}$）=$\frac{{3\sqrt{13}}}{13}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．△ABC中，角A，B，C的对分别为a，b，c，且a（1+cosC）+c（1+cosA）=3b．
    （1）求证：a，b，c成等差数列；
    （2）求cosB的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．在{an}为等比数列，a1=12，a2=24，则a3=（　　）
    A．36B．48C．60D．72

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

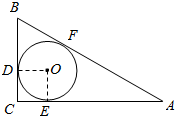    11．如图，在Rt△ABC中，∠C=90°，BC=a，AC=b，AB=c，⊙O为ABC的内切圆，D，E，F分别为切点，O的半径为r，试用含a，b，c的代数式表示r．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    18．函数f（x）=2x-$\frac{1}{x}$的单调递增区间是（-∞，0）．（0，+∞）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．若奇函数f（x）是定义在（-1，1）上的奇函数，且在[0，1）上递增，解关于a的不等式：f（a-2）+f（a2-4）＜0．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．过点P（3，4）作圆（x-1）2+y2=1的切线，切点为A，B，则直线AB的方程为2x+4y-3=0．

    查看答案和解析>>

    同步练习册答案