【题目】某校学生会为了了解学生对于“趣味运动会”的满意程度，从高一、高二两个年级分别随机调查了20个学生，得到学生对“趣味运动会”所设项目的满意度评分如下：
高一：62 7381 92 9585 74 6453 76
7886 95 6697 78 8882 76 89
高二：73 8362 51 9146 53 7364 82
9348 65 8174 56 5476 65 79
（1）根据两组数据完成两个年级满意度评分的茎叶图，并通过茎叶图比较两个年级满意度评分的平均值及离散程度（不要求计算出具体值，给出结论即可）；
高一 | 茎 | 高二 | ||||||||||
4 | ||||||||||||
3 | 5 | |||||||||||
6 | 4 | 2 | 6 | |||||||||
6 | 8 | 8 | 6 | 4 | 3 | 7 | ||||||
9 | 2 | 8 | 6 | 5 | 1 | 8 | ||||||
7 | 5 | 5 | 2 | 9 | ||||||||
（2）根据学生满意度评分，将学生的满意度从低到高分为三个等级：
满意度评分 | 低于70分 | 70分到89分 | 不低于90分 |
满意度等级 | 不满意 | 满意 | 非常满意 |
假设两个年级的评价结果相互独立．根据所给数据，以事件发生的频率作为相应事件发生的概率．随机调查高一、高二各一名学生，记事件A：“高一、高二学生都非常满意”，事件B：“高一的满意度等级高于高二的满意度等级”．分别求事件A、事件B的概率．
【答案】
（1）解：根据两组数据完成两个年级满意度评分的茎叶图如下：
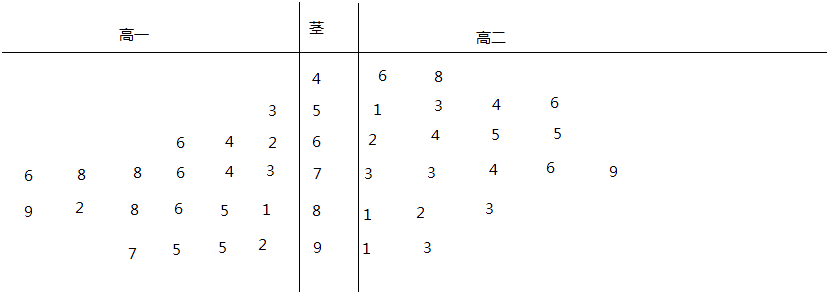
由茎叶图，得：
高一满意度评分的平均值为： 
= 
（53+62+64+66+73+74+76+78+78+76+81+85+86+88+82+89+92+95+95+97）=79.5，
高二满意度评分的平均值为： 
= （46+48+51+53+54+56+62+64+65+65+73+73+74+76+79+81+82+83+91+93）=68.45，
∴高二年级满意度评分的平均值比高一年级满意度评分的平均值低；高一年级满意度评分较集中．
（2）解：随机调查高一、高二各一名学生，
记事件A：“高一、高二学生都非常满意”，
∴事件A的概率P（A）= 
= 
，
事件B：“高一的满意度等级高于高二的满意度等级”，
∴事件B的概率P（B）= 
= 
．
【解析】（1）根据两组数据完成两个年级满意度评分能做出茎叶图，由茎叶图，能比较两个年级满意度评分的平均值及离散程度．（2）随机调查高一、高二各一名学生，由茎叶图能求出“高一、高二学生都非常满意”，和“高一的满意度等级高于高二的满意度等级”的概率．
阅读快车系列答案科目：高中数学 来源： 题型：
【题目】已知函数
，
，其中
.
（1）当
时，求函数
的值域
（2）当
时，设
，若给定
，对于两个大于1的正数
，存在
满足：
，使
恒成立，求实数的取值范围.
（3）当
时，设
，若
的最小值为
，求实数
的值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知矩形
，
，
，将
沿矩形的对角线
所在的直线进行翻折，在翻折过程中，则（ ）．
A. 当
时，存在某个位置，使得
B. 当
时，存在某个位置，使得
C. 当
时，存在某个位置，使得
D. 
时，都不存在某个位置，使得
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】平面直角坐标系中,已知曲线
,将曲线
上所有点横坐标,纵坐标分别伸长为原来的
倍和
倍后,得到曲线
(1)试写出曲线的参数方程;
(2)在曲线上求点
,使得点到直线
的距离最大,并求距离最大值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】供电部门对某社区
位居民2017年12月份人均用电情况进行统计后，按人均用电量分为
， 
， 
， 
， 
五组，整理得到如下的频率分布直方图，则下列说法错误的是
A. 
月份人均用电量人数最多的一组有
人
B. 月份人均用电量不低于
度的有
人
C. 月份人均用电量为
度
D. 在这位居民中任选
位协助收费，选到的居民用电量在一组的概率为
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某大学艺术专业400名学生参加某次测评，根据男女学生人数比例，使用分层抽样的方法从中随机抽取了100名学生，记录他们的分数，将数据分成7组：[20,30），[30,40），┄，[80,90]，并整理得到如下频率分布直方图：
（Ⅰ）从总体的400名学生中随机抽取一人，估计其分数小于70的概率；
（Ⅱ）已知样本中分数小于40的学生有5人，试估计总体中分数在区间[40,50）内的人数；
（Ⅲ）已知样本中有一半男生的分数不小于70，且样本中分数不小于70的男女生人数相等．试估计总体中男生和女生人数的比例．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知圆心在
轴上的圆
与直线
切于点
.
（1）求圆
的标准方程；
（2）已知
，经过原点，且斜率为正数的直线
与圆
交于
两点.
（ⅰ）求证： 
为定值；
（ⅱ）求
的最大值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知
两点分别在
轴和
轴上运动，且
，若动点
满足
.
（1）求出动点P的轨迹对应曲线C的标准方程；
（2）一条纵截距为2的直线
与曲线C交于P，Q两点，若以PQ直径的圆恰过原点，求出直线方程.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】对于定义在区间D上的函数f(x)，若存在闭区间[a，b]D和常数c，使得对任意x1∈[a，b]，都有f(x1)＝c，且对任意x2∈D，当x2[a，b]时，f(x2)＜c恒成立，则称函数f(x)为区间D上的“平顶型”函数．给出下列结论：
①“平顶型”函数在定义域内有最大值；
②函数f(x)＝x－|x－2|为R上的“平顶型”函数；
③函数f(x)＝sin x－|sin x|为R上的“平顶型”函数；
④当t≤
时，函数f(x)＝
是区间[0，＋∞)上的“平顶型”函数．
其中正确的结论是________．(填序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com