
【题目】已知![]() ,
,![]() ,其中常数
,其中常数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的极值;
的极值;
(2)若函数![]() 有两个零点
有两个零点![]() ,求实数
,求实数![]() 的范围;
的范围;
(3)设![]() ,在区间
,在区间![]() 内是否存在区间
内是否存在区间![]() ,使函数
,使函数![]() 在区间
在区间![]() 的值域也是
的值域也是![]() ?请给出结论,并说明理由.
?请给出结论,并说明理由.
【答案】(1)极小值0,没有极大值;(2)![]() ;(3)不存在区间
;(3)不存在区间![]() 符合要求,理由见解析.
符合要求,理由见解析.
【解析】
(1)求出导函数,利用导数研究函数的单调性,求出极值;
(2)求出导函数,利用导数研究函数的单调性,极值,得到有两个零点的条件,求出![]() 的范围;
的范围;
(3)先根据导数判断![]() 在
在![]() 单调递增,将
单调递增,将![]() 在区间
在区间![]() 的值域也是
的值域也是![]() ,转化为
,转化为![]() 有两个大于
有两个大于![]() 的不等实根解决问题.
的不等实根解决问题.
函数![]() 的定义域为
的定义域为![]() ,
,
(1)当![]() 时,
时,![]() ,
,![]() ,
,
而![]() 在
在![]() 上单调递增,又
上单调递增,又![]() ,
,
当![]() 时,
时,![]() ,则
,则![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,
时,![]() ,则
,则![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() 有极小值
有极小值![]() ,没有极大值.
,没有极大值.
(2)令![]() ,
, ![]() ,因为
,因为![]() ,所以
,所以
|
|
|
|
|
| 0 |
|
| 增 | 减 |
因为![]() 有两个零点,所以
有两个零点,所以![]() ,所以
,所以![]()
当![]() 时因为
时因为![]() ,
,![]() ,所以
,所以![]() 有两个零点.
有两个零点.
(3)![]() ,假设在区间
,假设在区间![]() 内是存在区间
内是存在区间![]() ,使函数
,使函数![]() 在区间
在区间![]() 的值域也是
的值域也是![]() ,因为
,因为![]() ,当
,当![]() 时
时![]()
所以![]() 在
在![]() 上是增函数,所以
上是增函数,所以![]() ,即
,即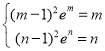
即方程![]() 有两个大于
有两个大于![]() 的不等实根.上述方程等价于
的不等实根.上述方程等价于![]()
设![]() ,所以
,所以![]()
所以![]() 在
在![]() 上是增函数,所以
上是增函数,所以![]()
![]() 上至多一个实数根.
上至多一个实数根.
即![]()
![]() 上不可能有两个不等实数根,所以假设不成立,所以不存在区间
上不可能有两个不等实数根,所以假设不成立,所以不存在区间![]() 符合要求.
符合要求.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点![]() ,且其离心率为
,且其离心率为![]() ,过坐标原点
,过坐标原点![]() 作两条互相垂直的射线与椭圆
作两条互相垂直的射线与椭圆![]() 分别相交于
分别相交于![]() ,
,![]() 两点.
两点.
(1)求椭圆![]() 的方程;
的方程;
(2)是否存在圆心在原点的定圆与直线![]() 总相切?若存在,求定圆的方程;若不存在,请说明理由.
总相切?若存在,求定圆的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】动点![]() 到点
到点![]() 的距离与到直线
的距离与到直线![]() 的距离的比值为
的距离的比值为![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 与点
与点![]() 的轨迹
的轨迹![]() 交于两点
交于两点![]() ,
,![]() ,设点
,设点![]() ,
,![]() 到直线
到直线![]() 的距离分别为
的距离分别为![]() ,
,![]() ,当
,当![]() 时,求直线
时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在测试中,客观题难题的计算公式为![]() ,其中
,其中![]() 为第
为第![]() 题的难度,
题的难度, ![]() 为答对该题的人数,
为答对该题的人数, ![]() 为参加测试的总人数.现对某校高三年级120名学生进行一次测试,共5道客观题.测试前根据对学生的了解,预估了每道题的难度,如下表所示:
为参加测试的总人数.现对某校高三年级120名学生进行一次测试,共5道客观题.测试前根据对学生的了解,预估了每道题的难度,如下表所示:

测试后,从中随机抽取了10名学生,将他们编号后统计各题的作答情况,如下表所示(“√”表示答对,“×”表示答错):
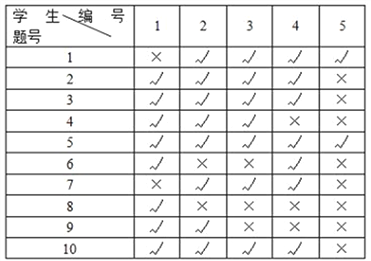
(1)根据题中数据,将抽样的10名学生每道题实测的答对人数及相应的实测难度填入下表,并估计这120名学生中第5题的实测答对人数;

(2)从编号为1到5的5人中随机抽取2人,求恰好有1人答对第5题的概率;
(3)定义统计量![]() ,其中
,其中![]() 为第
为第![]() 题的实测难度,
题的实测难度, ![]() 为第
为第![]() 题的预估难度(
题的预估难度(![]() ).规定:若
).规定:若![]() ,则称该次测试的难度预估合理,否则为不合理.判断本次测试的难度预估是否合理.
,则称该次测试的难度预估合理,否则为不合理.判断本次测试的难度预估是否合理.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为广泛开展垃圾分类的宣传教育和倡导工作,使市民树立垃圾分类的环保意识,学会垃圾分类的知识,特举办了“垃圾分类知识竞赛".据统计,在为期1个月的活动中,共有两万人次参与网络答题.市文明实践中心随机抽取100名参与该活动的市民,以他们单次答题得分作为样本进行分析,由此得到如图所示的频率分布直方图:

(1)求图中a的值及参与该活动的市民单次挑战得分的平均成绩![]() (同一组中数据用该组区间中点值作代表);
(同一组中数据用该组区间中点值作代表);
(2)若垃圾分类答题挑战赛得分落在区间![]() 之外,则可获得一等奖奖励,其中
之外,则可获得一等奖奖励,其中![]() ,s分别为样本平均数和样本标准差,计算可得
,s分别为样本平均数和样本标准差,计算可得![]() ,若某人的答题得分为96分,试判断此人是否获得一等奖;
,若某人的答题得分为96分,试判断此人是否获得一等奖;
(3)为扩大本次“垃圾分类知识竞赛”活动的影响力,市文明实践中心再次组织市民组队参场有奖知识竞赛,竞赛共分五轮进行,已知“光速队”与“超能队”五轮的成绩如下表:
成绩 | 第一轮 | 第二轮 | 第三轮 | 第四轮 | 第五轮 |
“光速队” | 93 | 98 | 94 | 95 | 90 |
“超能队” | 93 | 96 | 97 | 94 | 90 |
①分别求“光速队”与“超能队”五轮成绩的平均数和方差;
②以上述数据为依据,你认为"光速队”与“超能队”的现场有奖知识竞赛成绩谁更稳定?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,椭圆
,椭圆![]() 上一点
上一点![]() 到左右两个焦点
到左右两个焦点![]() 、
、![]() 的距离之和是4.
的距离之和是4.
(1)求椭圆的方程;
(2)已知过![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]() 、
、![]() 两点,且两点与左右顶点不重合,若
两点,且两点与左右顶点不重合,若![]() ,求四边形
,求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知x与y之间的几组数据如表:
x | 1 | 2 | 3 | 4 |
y | 1 | m | n | 4 |
如表数据中y的平均值为2.5,若某同学对m赋了三个值分别为1.5,2,2.5,得到三条线性回归直线方程分别为![]() ,
,![]() ,
,![]() ,对应的相关系数分别为
,对应的相关系数分别为![]() ,
,![]() ,
,![]() ,下列结论中错误的是( )
,下列结论中错误的是( )
参考公式:线性回归方程![]() 中,其中
中,其中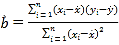 ,
,![]() .相关系数
.相关系数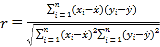 .
.
A.三条回归直线有共同交点B.相关系数中,![]() 最大
最大
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小区为了调查本小区业主对物业服务满意度的真实情况,对本小区业主进行了调查,调查中问了两个问题1:你的手机尾号是不是奇数?问题2:你是否满意物业的服务?调查者设计了一个随机化装置,其中装有大小、形状和质量完全相同的白球和红球,每个被调查者随机从装置中摸到红球和白球的可能性相同,其中摸到白球的业主回答第一个问题,摸到红球的业主回答第二个问题,回答“是”的人往一个盒子中放一个小石子,回答“否”的人什么都不要做由于问题的答案只有“是”和“否”,而且回答的是哪个问题别人并不知道,因此被调查者可以毫无顾虑地给出符合实际情况的答案.已知某小区80名业主参加了问卷,且有47名业主回答了“是”,由此估计本小区对物业服务满意的百分比大约为( )
A.85%B.75%C.63.5%D.67.5%
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com