
 ,tanθ>0,则cosθ=
,tanθ>0,则cosθ= ;
; 既是奇函数又是偶函数;
既是奇函数又是偶函数; ,tanθ>0,则必有cosθ<0,可判定真假;②根据函数的奇偶性可知区间[2a-1,a+4]应关于原点对称可求出a的值,再根据f(x)是偶函数求出b的值,可判定真假;③先化简f(x)可判定真假;④先求出x∈(-∞,0)时的函数解析式从而求出x∈R时的解析式,可判定真假.
,tanθ>0,则必有cosθ<0,可判定真假;②根据函数的奇偶性可知区间[2a-1,a+4]应关于原点对称可求出a的值,再根据f(x)是偶函数求出b的值,可判定真假;③先化简f(x)可判定真假;④先求出x∈(-∞,0)时的函数解析式从而求出x∈R时的解析式,可判定真假.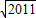 },且化简得f(x)=0,故是既奇又偶的函数;
},且化简得f(x)=0,故是既奇又偶的函数;

科目:高中数学 来源: 题型:
| π |
| 6 |
| 1 |
| 2 |
| π |
| 2 |
| π |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 2 |
| 2π |
| 7 |
| π |
| 2 |
| π |
| 2 |
| π |
| 3 |
2tan
| ||
1-tan2
|
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| π |
| 6 |
| 1 |
| 2 |
| π |
| 2 |
| π |
| 2 |
| 1 |
| 2 |
| A.4 | B.3 | C.2 | D.1 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
| π |
| 2 |
| 2π |
| 7 |
| π |
| 2 |
| π |
| 2 |
| π |
| 3 |
2tan
| ||
1-tan2
|
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2013年高考数学备考复习卷1:集合与常用逻辑用语(解析版) 题型:选择题
 ,则sin α=
,则sin α= ”的否命题是假命题;
”的否命题是假命题; +2kπ(k∈Z)”是“函数y=sin(2x+φ)为偶函数”的充要条件;
+2kπ(k∈Z)”是“函数y=sin(2x+φ)为偶函数”的充要条件; ),使sin x+cos x=
),使sin x+cos x= ”,命题q:“在△ABC中,若sin A>sin B,则A>B”,那么命题¬p∧q为真命题.
”,命题q:“在△ABC中,若sin A>sin B,则A>B”,那么命题¬p∧q为真命题.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com