
分析 由已知结合数列递推式可得数列{an}是递增数列,且an>0,进一步得到$\frac{1}{{a}_{n}+1}=\frac{1}{{a}_{n}}-\frac{1}{{a}_{n+1}}$,可得$\frac{1}{{{a_1}+1}}+\frac{1}{{{a_2}+1}}+…+\frac{1}{{{a_{2016}}+1}}$<1,结合已知定义得答案.
解答 解:∵a1=1,an+1=an2+an>0,
∴数列{an}是递增数列,且an>0,
则由an+1=an2+an,得$\frac{1}{{a}_{n}+1}=\frac{1}{{a}_{n}}-\frac{1}{{a}_{n+1}}$,
∴$\frac{1}{{{a_1}+1}}+\frac{1}{{{a_2}+1}}+…+\frac{1}{{{a_{2016}}+1}}$
=$\frac{1}{{a}_{1}}-\frac{1}{{a}_{2}}+\frac{1}{{a}_{2}}-\frac{1}{{a}_{3}}+…+$$\frac{1}{{a}_{2016}}-\frac{1}{{a}_{2017}}$
=$\frac{1}{{a}_{1}}-\frac{1}{{a}_{2017}}<\frac{1}{{a}_{1}}=1$,
又$\frac{1}{{a}_{1}+1}+\frac{1}{{a}_{2}+1}+…+\frac{1}{{a}_{2016}+1}>0$,
∴[$\frac{1}{{{a_1}+1}}+\frac{1}{{{a_2}+1}}+…+\frac{1}{{{a_{2016}}+1}}$]=0.
故答案为:0.
点评 本题考查数列递推式,关键是由数列递推式得到$\frac{1}{{a}_{n}+1}=\frac{1}{{a}_{n}}-\frac{1}{{a}_{n+1}}$,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | {2,4} | B. | {1,2,4} | C. | {2,3,4,5} | D. | {1,2,3,4,5} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
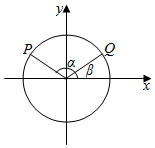 [重点中学做]如图所示,以Ox为始边作角α与β(0<β<α<π),它们的终边分别与单位圆相交于点P、Q,已知点P的横坐标为-$\frac{4}{5}$.
[重点中学做]如图所示,以Ox为始边作角α与β(0<β<α<π),它们的终边分别与单位圆相交于点P、Q,已知点P的横坐标为-$\frac{4}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{63}$ | B. | $\frac{1}{31}$ | C. | $\frac{3}{61}$ | D. | $\frac{1}{15}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 为绘制海底地貌图,测量海底两点C,D之间的距离,海底探测仪沿水平方向在A,B两点进行测量,A,B,C,D在同一个铅垂平面内,海底探测仪测得∠BAC=30°,∠DAC=45°,∠ABD=45°,∠DBC=75°,A,B两点的距离为$\sqrt{3}$海里,则C,D之间的距离为( )
为绘制海底地貌图,测量海底两点C,D之间的距离,海底探测仪沿水平方向在A,B两点进行测量,A,B,C,D在同一个铅垂平面内,海底探测仪测得∠BAC=30°,∠DAC=45°,∠ABD=45°,∠DBC=75°,A,B两点的距离为$\sqrt{3}$海里,则C,D之间的距离为( )| A. | $\sqrt{5}$海里 | B. | 2海里 | C. | $\frac{\sqrt{6}+\sqrt{2}}{2}$海里 | D. | $\sqrt{2}$+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x=-1 | B. | x=-$\frac{1}{2}$ | C. | x=1 | D. | x=$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com