科目：高中数学 来源：2016-2017学年安徽省阜阳市高二1月学科竞赛数学（理）试卷（解析版） 题型：解答题
某企业生产甲、乙两种产品均需用
两种原料.已知生产1吨每种产品需原料及每天原料的可用限额如表所示：
（1）设该企业每天生产甲、乙两种产品分别为
吨，试写出关于
的线性约束条件并画出可行域；
（2）如果生产1吨甲、乙产品可获利润分别为3万元、4万元，试求该企业每天可获得的最大利润.
查看答案和解析>>
科目：高中数学 来源：2017届江西省、临川一中高三1月联考数学（文）试卷（解析版） 题型：解答题
已知函数
，在x=1处的切线与直线
垂直，函数
．
(1)求实数
的值；
(2)设
是函数
的两个极值点，记
，若
，
①
的取值范围；②求
的最小值．
查看答案和解析>>
科目：高中数学 来源：2017届江西省、临川一中高三1月联考数学（文）试卷（解析版） 题型：选择题
“微信抢红包”自2015年以来异常火爆，在某个微信群某次进行的抢红包活动中，若所发红包的总金额为9元，被随机分配为1.49元，1.31元，2.19元，3.40元，0.61元，共5份，供甲、乙等5人抢，每人只能抢一次，则甲、乙二人抢到的金额之和不低于4元的概率是（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中数学 来源：2017届江西省、临川一中高三1月联考数学（理）试卷（解析版） 题型：解答题
已知右焦点为
的椭圆
与直线
相交于
、
两点，且
.
（1）求椭圆
的方程；
（2）
为坐标原点，
，
，
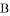是椭圆
上不同的三点，并且
为
的重心，试探究的面积是否为定值，若是，求出这个定值；若不是，说明理由.
查看答案和解析>>
科目：高中数学 来源：2017届广东省深圳市高三下学期第一次调研考试（一模）数学（文）试卷（解析版） 题型：解答题
设
为数列
的前
项和，且
．
（1）求数列
的通项公式；
（2）求数列
的前项和
．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
满足约束条件
，则
的取值范围是______________
中,
,
为
边上的点
,若
,则
的最大值是( )
B. 
C. 
D. 
,
,
的大小关系为（ ）
B. 
C. 
D. 
（ ）
B. 
C. 
D. 