【答案】
分析:(I)据导数的几何意义求出函数f(x)在x=1处的导数,从而求出切线的斜率,再根据两直线垂直建立等式关系,解之即可.
(II)当x=0时,显然f(x)=e
x>0恒成立;当x大于0时,令f(x)大于0,解出a大于一个函数,设这个函数为Q(x),求出Q(x)的导函数,分x大于0小于1和x大于1两种情况讨论导函数的正负,进而得到函数的增减性,根据函数的增减性得到Q(x)的最大值,即可得到a的取值范围;
(III)把f(x)和g(x)的解析式代入y中确定出y的解析式,设M(x)为y的解析式,求出M(x)的导函数,h(x)=
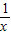
+lnx-1,求出h(x)的导函数,由x的范围得到导函数为正数,进而得到h(x)在[1,e]上为增函数,得到h(1)为最小值,即可得到M(x)的最小值,而曲线C:y=g(x)-f(x)在点x=x
处的切线与y轴垂直,即切线的斜率为0,即导函数的值为0,与导函数的最小值为1矛盾,所以不存在实数x
∈[1,e],使曲线C:y=g(x)-f(x)在点x=x
处的切线与y轴垂直.
解答:解:(Ⅰ)f'(x)=e
x+a,(1分)
因此y=f(x)在(1,f(1))处的切线l的斜率为e+a,(2分)
又直线x+(e-1)y=1的斜率为
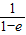
,(3分)
∴(e+a)
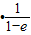
=-1,
∴a=-1.(5分)
(Ⅱ)∵当x≥0时,f(x)=e
x+ax>0恒成立,
∴先考虑x=0,此时,f(x)=e
x,a可为任意实数;(6分)
又当x>0时,f(x)=e
x+ax>0恒成立,
则
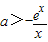
恒成立,(7分)
设h(x)=
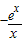
,则h'(x)=
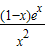
,
当x∈(0,1)时,h'(x)>0,h(x)在(0,1)上单调递增,
当x∈(1,+∞)时,h'(x)<0,h(x)在(1,+∞)上单调递减,
故当x=1时,h(x)取得极大值,h(x)
max=h(1)=-e,(9分)
∴要使x≥0,f(x)>0恒成立,a>-e,
∴实数a的取值范围为(-e,+∞).(10分)
(Ⅲ)依题意,曲线C的方程为y=e
xlnx-e
x+x,
令u(x)=e
xlnx-e
x+x,则
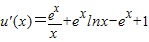
=
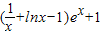
设
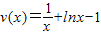
,则
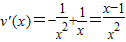
,
当x∈[1,e],v'(x)≥0,故v(x)在[1,e]上的最小值为v(1)=0,(12分)
所以v(x)≥0,又e
x>0,∴
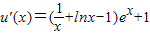
>0,
而若曲线C:y=g(x)-f(x)在点x=x
处的切线与y轴垂直,
则u'(x
)=0,矛盾.(13分)
所以,不存在实数x
∈[1,e],使曲线C:y=g(x)-f(x)在点x=x
处的切线与y轴垂直.
点评:此题考查学生会利用导数求曲线上过某点切线方程的斜率,掌握两条直线垂直的判定,掌握导数在最大值、最小值中的运用,是一道中档题.

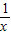 +lnx-1,求出h(x)的导函数,由x的范围得到导函数为正数,进而得到h(x)在[1,e]上为增函数,得到h(1)为最小值,即可得到M(x)的最小值,而曲线C:y=g(x)-f(x)在点x=x处的切线与y轴垂直,即切线的斜率为0,即导函数的值为0,与导函数的最小值为1矛盾,所以不存在实数x∈[1,e],使曲线C:y=g(x)-f(x)在点x=x处的切线与y轴垂直.
+lnx-1,求出h(x)的导函数,由x的范围得到导函数为正数,进而得到h(x)在[1,e]上为增函数,得到h(1)为最小值,即可得到M(x)的最小值,而曲线C:y=g(x)-f(x)在点x=x处的切线与y轴垂直,即切线的斜率为0,即导函数的值为0,与导函数的最小值为1矛盾,所以不存在实数x∈[1,e],使曲线C:y=g(x)-f(x)在点x=x处的切线与y轴垂直.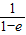 ,(3分)
,(3分)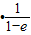 =-1,
=-1,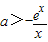 恒成立,(7分)
恒成立,(7分)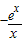 ,则h'(x)=
,则h'(x)=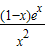 ,
,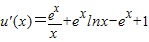 =
=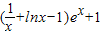
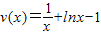 ,则
,则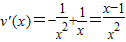 ,
,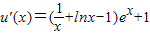 >0,
>0,

 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案