
【题目】《九章算术》是我国古代内容极为丰富的数学名著,书中将底面为直角三角形的直棱柱称为堑堵,将底面为矩形的棱台称为刍童.在如图所示的堑堵![]() 与刍童
与刍童![]() 的组合体中
的组合体中![]() ,
,![]() .台体体积公式:
.台体体积公式:![]() ,其中
,其中![]() 分别为台体上、下底面面积,
分别为台体上、下底面面积,![]() 为台体高.
为台体高.
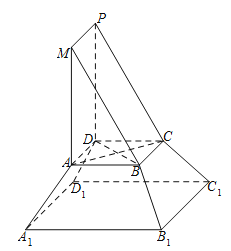
(Ⅰ)证明:直线![]()
![]() 平面
平面![]() ;
;
(Ⅱ)若![]() ,
,![]() ,
,![]() ,三棱锥
,三棱锥![]() 的体积
的体积![]() ,求该组合体的体积.
,求该组合体的体积.
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】网络购物已经成为一种时尚,电商们为了提升知名度,加大了在媒体上的广告投入.经统计,近五年某电商在媒体上的广告投入费用x(亿元)与当年度该电商的销售收入y(亿元)的数据如下表:):
年份 | 2012年 | 2013年 | 2014 | 2015 | 2016 |
广告投入x | 0.8 | 0.9 | 1 | 1.1 | 1.2 |
销售收入y | 16 | 23 | 25 | 26 | 30 |
(1)求y关于x的回归方程; (2)2017年度该电商准备投入广告费1.5亿元,
利用(1)中的回归方程,预测该电商2017年的销售收入.
附:回归直线的斜率和截距的最小二乘估计公式分别为: 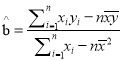
![]() ,选用数据:
,选用数据: ![]() ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=2sin(x-![]() )-
)-![]() ,现将f(x)的图象向左平移
,现将f(x)的图象向左平移![]() 个单位长度,再向上平移
个单位长度,再向上平移![]() 个单位长度,得到函数g(x)的图象.
个单位长度,得到函数g(x)的图象.
(1)求f(![]() )+g(
)+g(![]() )的值;
)的值;
(2)若a,b,c分别是△ABC三个内角A,B,C的对边,a+c=4,且当x=B时,g(x)取得最大值,求b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的定义域为(-2,2),函数g(x)=f(x-1)+f(3-2x).
(1)求函数g(x)的定义域;
(2)若f(x)是奇函数,且在定义域上单调递减,求不等式g(x)≤0的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知长方体ABCD-A1B1C1D1的对称中心在坐标原点,交于同一顶点的三个面分别平行于三个坐标平面,顶点A(-2,-3,-1),求其他七个顶点的坐标.
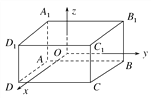
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知![]() 是半圆
是半圆![]() 的直径,
的直径,![]() ,
,![]() 是将半圆圆周四等分的三个分点.
是将半圆圆周四等分的三个分点.

(1)从![]() 这5个点中任取3个点,求这3个点组成直角三角形的概率;
这5个点中任取3个点,求这3个点组成直角三角形的概率;
(2)在半圆内任取一点![]() ,求
,求![]() 的面积大于
的面积大于![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017届江西省南昌市高三第一次模拟考试数学(理)】已知函数![]() (
(![]() ,
,![]() 是自然对数的底数).
是自然对数的底数).
(1)若![]() 是
是![]() 上的单调递增函数,求实数
上的单调递增函数,求实数![]() 的取值范围;
的取值范围;
(2)当![]() 时,证明:函数
时,证明:函数![]() 有最小值,并求函数
有最小值,并求函数![]() 最小值的取值范围.
最小值的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017届陕西省西安市铁一中学高三上学期第五次模拟考试数学(文)】已知向量![]() ,
,![]() ,且函数
,且函数![]() .
.
(Ⅰ)当函数在![]() 上的最大值为3时,求
上的最大值为3时,求的值;
(Ⅱ)在(Ⅰ)的条件下,若对任意的![]() ,函数
,函数,![]() 的图像与直线
的图像与直线有且仅有两个不同的交点,试确定的值.并求函数在上的单调递减区间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com