
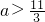 ;
;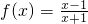 ,设f2(x)=f[f(x)],f3(x)=f[f2(x)],…,fn+1(x)=f[fn(x)](n∈N*且n≥2),令集合M={x|f2009(x)=x,x∈R},则集合M为空集.
,设f2(x)=f[f(x)],f3(x)=f[f2(x)],…,fn+1(x)=f[fn(x)](n∈N*且n≥2),令集合M={x|f2009(x)=x,x∈R},则集合M为空集. 对于任意x∈(1,3)恒成立,x+
对于任意x∈(1,3)恒成立,x+ ≥2
≥2 等号当且仅当x=
等号当且仅当x= =
= 时成立,又当x=1,x+
时成立,又当x=1,x+ =3,x=3,x+
=3,x=3,x+ =
= ,故a≥
,故a≥ 故不对.
故不对.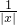 ,x∈R恒成立,这是不可能的,故不对.
,x∈R恒成立,这是不可能的,故不对. ,f3(x)=
,f3(x)= ,f4(x)=
,f4(x)= ,f5(x)=
,f5(x)=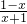 f6(x)=-x,f7(x)=f3(x)=
f6(x)=-x,f7(x)=f3(x)= ,故从f3(x)开始组成了一个以f3(x)为首项,以周期为4重复出现,由2009=3+501*4+2得f2009(x)=f5(x),故
,故从f3(x)开始组成了一个以f3(x)为首项,以周期为4重复出现,由2009=3+501*4+2得f2009(x)=f5(x),故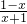 =x整理得,x2+2x-1=0,有解,故不对.
=x整理得,x2+2x-1=0,有解,故不对.

科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| x-1 |
| x+1 |
| 11 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com