
【题目】已知函数f(x)=cos(![]() +x)cos(
+x)cos(![]() -x),g(x)=
-x),g(x)=![]() sin 2x-
sin 2x-![]() .
.
(1)求函数f(x)的最小正周期;
(2)求函数h(x)=f(x)-g(x)的最大值,并求使h(x)取得最大值的x的集合.
【答案】(1)π;(2)h(x)取得最大值![]() ,对应的x的集合为{x|x=kπ-
,对应的x的集合为{x|x=kπ-![]() ,k∈Z}.
,k∈Z}.
【解析】试题分析:(1)利用两角和与差的余弦公式及二倍角公式,化简得f(x)=![]() cos 2x-
cos 2x-![]() ,,结合三角函数的周期公式即可算出函数f(x)的最小正周期;
,,结合三角函数的周期公式即可算出函数f(x)的最小正周期;
(2)根据(1)中化简的结果,得h(x)=![]() cos
cos![]() ,再由三角函数的图象与性质吗,即可得到使得h(x)取得最大值的x的集合.
,再由三角函数的图象与性质吗,即可得到使得h(x)取得最大值的x的集合.
试题解析:
(1)f(x)=cos![]() cos
cos![]()
=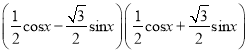
=![]() cos2x-
cos2x-![]() sin2x=
sin2x=![]() -
-![]() =
=![]() cos 2x-
cos 2x-![]() ,
,
所以f(x)的最小正周期为![]() =π.
=π.
(2)h(x)=f(x)-g(x)=![]() cos 2x-
cos 2x-![]() sin 2x=
sin 2x=![]() cos
cos![]() ,
,
当2x+![]() =2kπ,即x=-
=2kπ,即x=-![]() +kπ(k∈Z)时,h(x)取得最大值
+kπ(k∈Z)时,h(x)取得最大值![]() .
.
所以h(x)取得最大值时,对应的x的集合为{x|x=kπ-![]() ,k∈Z}.
,k∈Z}.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,如图描述了甲、乙、丙三辆汽车在不同速度下燃油效率情况,下列叙述中正确的是( ) 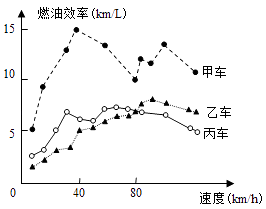
A.消耗1升汽油,乙车最多可行驶5千米
B.以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多
C.甲车以80千米/小时的速度行驶1小时,消耗10升汽油
D.某城市机动车最高限速80千米/小时,相同条件下,在该市用丙车比用乙车更省油
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在经济学中,函数f(x)的边际函数为Mf(x),定义为Mf(x)=f(x+1)﹣f(x).已知某服装公司每天最多
生产100件.生产x件的收入函数为R(x)=300x﹣2x2(单位元),其成本函数为C(x)=50x+300(单位:元),利润等于收入与成本之差.
(1)求出利润函数p(x)及其边际利润函数Mp(x);
(2)分别求利润函数p(x)及其边际利润函数Mp(x)的最大值;
(3)你认为本题中边际利润函数Mp(x)最大值的实际意义是什么?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若抛物线y2=2px(p>0)上一点到焦点和抛物线对称轴的距离分别为10和6,则抛物线方程为( )
A.y2=4x
B.y2=36x
C.y2=4x或y2=36x
D.y2=8x或y2=32x
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求函数的定义域;
(2)判断函数的奇偶性,并证明你的结论;
(3)在函数![]() 图像上是否存在两个不同的点
图像上是否存在两个不同的点![]() ,使直线
,使直线![]() 垂直
垂直![]() 轴,若存在,求出
轴,若存在,求出![]() 两点坐标;若不存在,说明理由.
两点坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 的方程为:
的方程为: ![]() 。
。
(1)求圆![]() 的圆心所在直线方程一般式;
的圆心所在直线方程一般式;
(2)若直线![]() 被圆
被圆![]() 截得弦长为
截得弦长为![]() ,试求实数
,试求实数![]() 的值;
的值;
(3)已知定点![]() ,且点
,且点![]() 是圆
是圆![]() 上两动点,当
上两动点,当![]() 可取得最大值为
可取得最大值为![]() 时,求满足条件的实数
时,求满足条件的实数![]() 的值。
的值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阿波罗尼斯是古希腊著名数学家,与欧几里得、阿基米德被称为亚历山大时期数学三巨匠,他对圆锥曲线有深刻而系统的研究,主要研究成果集中在他的代表作《圆锥曲线》一书,阿波罗尼斯圆是他的研究成果之一,指的是:已知动点M与两定点A、B的距离之比为λ(λ>0,λ≠1),那么点M的轨迹就是阿波罗尼斯圆.下面,我们来研究与此相关的一个问题.已知圆:x2+y2=1和点 ![]() ,点B(1,1),M为圆O上动点,则2|MA|+|MB|的最小值为( )
,点B(1,1),M为圆O上动点,则2|MA|+|MB|的最小值为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com