
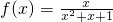 ,④f(x)是定义在R上的奇函数,且满足对一切实数x1,x2均有|f(x1)-f(x2)|≤2012|x1-x2|,⑤
,④f(x)是定义在R上的奇函数,且满足对一切实数x1,x2均有|f(x1)-f(x2)|≤2012|x1-x2|,⑤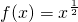 ,其中是F函数的有________.
,其中是F函数的有________.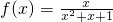 ,∴要使|f(x)|≤m|x|成立,
,∴要使|f(x)|≤m|x|成立,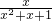 |≤m|x|,
|≤m|x|,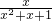 |的最大值.
|的最大值. )2+
)2+ ≥
≥ ,
, 时,
时,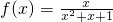 是F函数,故③是F函数;
是F函数,故③是F函数;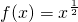 ,∴|f(x)|≤m|x|不成立,故⑤不是F函数.
,∴|f(x)|≤m|x|不成立,故⑤不是F函数.

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| π | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com