
| A. | (-3,1) | B. | $(\frac{3}{2},+∞)$ | C. | (-3,1)∪$(\frac{3}{2},+∞)$ | D. | $(-3,\frac{3}{2})$ |
分析 当x≤1时,f(x)=2x+1为增函数,则f(x)>1,当x>1时,f(x)=1-log2x为减函数,则f(x)<1,满足不等式f(1-m2)>f(2m-2),化为关于m的不等式组,解得即可.
解答 解:当x≤1时,f(x)=2x+1为增函数,则f(x)≥1,
当x>1时,f(x)=1-log2x为减函数,则f(x)<1,
∵f(1-m2)>f(2m-2),
∴$\left\{\begin{array}{l}{1-{m}^{2}≤1}\\{2m-2≤1}\\{1-{m}^{2}>2m-2}\end{array}\right.$或$\left\{\begin{array}{l}{1-{m}^{2}>1}\\{2m-2>1}\\{1-{m}^{2}<2m-2}\end{array}\right.$或$\left\{\begin{array}{l}{1-{m}^{2}≤1}\\{2m-2>1}\\{1-{m}^{2}>2m-2}\end{array}\right.$,
解得-3<m<1或x>$\frac{3}{2}$,
故选:C.
点评 本题考查了分段函数和不等式组的解集,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
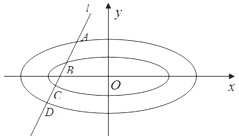 已知椭圆C1,C2均为中心在原点,焦点在x轴上的椭圆,离心率均为$\frac{{\sqrt{2}}}{2}$,其中C1的焦点坐标分别为(-1,0),(1,0),C2的左右顶点坐标为(-2,0),(2,0).
已知椭圆C1,C2均为中心在原点,焦点在x轴上的椭圆,离心率均为$\frac{{\sqrt{2}}}{2}$,其中C1的焦点坐标分别为(-1,0),(1,0),C2的左右顶点坐标为(-2,0),(2,0).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
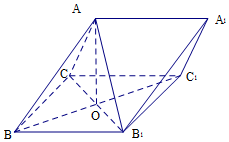 如图,在三棱柱ABC-A1B1C1中,侧面BB1C1C 为菱形,B1C与BC1交于点O,AO⊥平面BB1C1C
如图,在三棱柱ABC-A1B1C1中,侧面BB1C1C 为菱形,B1C与BC1交于点O,AO⊥平面BB1C1C查看答案和解析>>
科目:高中数学 来源: 题型:解答题
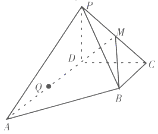 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,Q为AD的中点,M是棱PC的中点,PA=PD=PC,BC=$\frac{1}{2}$AD=2,CD=4
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,Q为AD的中点,M是棱PC的中点,PA=PD=PC,BC=$\frac{1}{2}$AD=2,CD=4查看答案和解析>>
科目:高中数学 来源: 题型:解答题
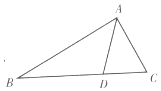 如图,在△ABC中,$AB=2AC,cosB=\frac{{2\sqrt{5}}}{5}$,点D在线段BC上.
如图,在△ABC中,$AB=2AC,cosB=\frac{{2\sqrt{5}}}{5}$,点D在线段BC上.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $y=-\frac{3}{4}$ | C. | $y=\frac{1}{12}$ | D. | $y=-\frac{1}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)的图象关于($\frac{π}{12}$,1)中心对称 | B. | f(x)在($\frac{5π}{12}$,$\frac{11π}{12}$)上单调递减 | ||
| C. | f(x)的图象关于x=$\frac{π}{3}$对称 | D. | f(x)的最大值为3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com