
已知命题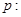 “椭圆
“椭圆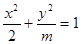 的焦点在
的焦点在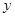 轴上”;
轴上”;
命题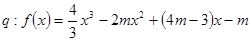 在
在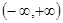 上单调递增,若“
上单调递增,若“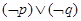 ”为假,求
”为假,求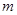 的取值范围.
的取值范围.
【解析】主要考查了命题中复合命题的真值问题的判定,以及椭圆,导数的运用。
首先求解若p为真,则m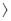 2.
2.
若q为真,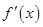 =
=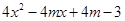
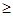 0在R上恒成立。
0在R上恒成立。
所以 
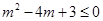 所以
所以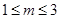
而要是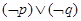 为假,则
为假,则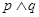 ,这样就可以得到了。
,这样就可以得到了。
若p为真,则m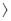 2.
2分
2.
2分
若q为真,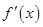 =
=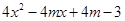
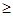 0在R上恒成立。
0在R上恒成立。
所以 
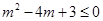 所以
所以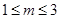 3分
3分
若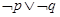 为假,所以
为假,所以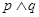 为真 2分
为真 2分
所以m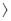 2且
2且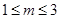 , 所以
, 所以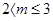
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源:2012-2013辽宁省五校协作体高二下学期学期初测试理科数学试卷 (解析版) 题型:解答题
已知命题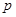 :
: 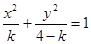 表示焦点在
表示焦点在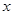 轴上的椭圆,命题
轴上的椭圆,命题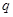 :
: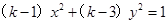 表示双曲线。若
表示双曲线。若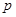 或
或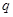 为真,
为真,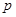 且
且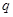 为假,求
为假,求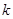 的取值范围。(10分)
的取值范围。(10分)
查看答案和解析>>
科目:高中数学 来源:2010-2011学年湖南省高二上学期质量检测数学理卷 题型:解答题
(本小题满分12分)已知命题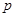 :
: 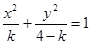 表示焦点在
表示焦点在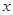 轴上的椭圆,命题
轴上的椭圆,命题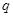 :
: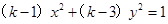 表示双曲线.若
表示双曲线.若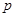 和
和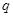 有且仅有一个正确,求
有且仅有一个正确,求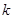 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2013届江苏省淮安市高二上学期期末模拟考试(四)数学 题型:解答题
已知命题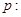 “方程
“方程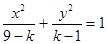 表示焦点在
表示焦点在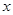 轴上的椭圆”,命题
轴上的椭圆”,命题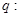 “方程
“方程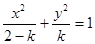 表示双曲线”.
表示双曲线”.
(1)若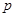 是真命题,求实数
是真命题,求实数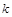 的取值范围;
的取值范围;
(2)若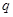 是真命题,求实数
是真命题,求实数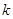 的取值范围;
的取值范围;
(3)若“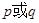 ”是真命题,求实数
”是真命题,求实数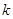 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com