
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,且点
,且点![]() 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)当点![]() 在椭圆
在椭圆![]() 的图像上运动时,点
的图像上运动时,点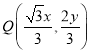 在曲线
在曲线![]() 上运动,求曲线
上运动,求曲线![]() 的轨迹方程,并指出该曲线是什么图形;
的轨迹方程,并指出该曲线是什么图形;
(3)过椭圆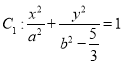 上异于其顶点的任意一点
上异于其顶点的任意一点![]() 作曲线
作曲线![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() 不在坐标轴上),若直线
不在坐标轴上),若直线![]() 在
在![]() 轴,
轴,![]() 轴上的截距分别为
轴上的截距分别为![]() 试问:
试问:![]() 是否为定值?若是,求出该定值;若不是,请说明理由.
是否为定值?若是,求出该定值;若不是,请说明理由.
【答案】(1)![]() (2)
(2)![]() ,曲线
,曲线![]() 的图形是一个以坐标原点为圆心、
的图形是一个以坐标原点为圆心、![]() 为半径的圆 (3)是定值,
为半径的圆 (3)是定值,![]()
【解析】
(1)由![]() 得
得![]() ,再把点
,再把点![]() 坐标代入又得一方程,联立后可解得
坐标代入又得一方程,联立后可解得![]() 得椭圆方程;
得椭圆方程;
(2)设![]() ,用
,用![]() 表示
表示![]() ,把
,把![]() 代入椭圆方程可得曲线
代入椭圆方程可得曲线![]() 方程,由方程可判断曲线形状;
方程,由方程可判断曲线形状;
(3)由(1)知,![]() 设点
设点![]() ,由
,由![]() 坐标可得切线方程,代入
坐标可得切线方程,代入![]() 点坐标于两切线方程后观察结论可得直线
点坐标于两切线方程后观察结论可得直线![]() 方程,求出
方程,求出![]() ,计算
,计算![]() ,利用
,利用![]() 在椭圆
在椭圆![]() 上可得.
上可得.
(1)由题意得,![]() 所以
所以![]()
又点![]() 在椭圆
在椭圆![]() 上,所以
上,所以![]() 解得
解得![]()
所以椭圆![]() 的标准方程为
的标准方程为![]()
(2)设![]() ,则
,则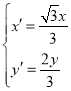 ,于是
,于是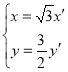 ,
,
由于点![]() 在椭圆
在椭圆![]() 的图像上,
的图像上,
所以 ![]() 即
即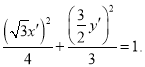
整理得![]() ,
,
所以曲线![]() 的轨迹方程为
的轨迹方程为![]()
曲线![]() 的图形是一个以坐标原点为圆心,
的图形是一个以坐标原点为圆心,![]() 为半径的圆.
为半径的圆.
(3)由(1)知,![]() 设点
设点![]()
则直线![]() 的方程为
的方程为![]() ①
①
直线![]() 的方程为
的方程为![]() ②
②
把点![]() 的坐标代入①②得
的坐标代入①②得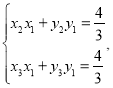
所以直线![]() 的方程为
的方程为![]()
令![]() 得
得![]() 令
令![]() 得
得![]()
所以![]() 又点
又点![]() 在椭圆
在椭圆![]() 上,
上,
所以![]() 即
即![]() 为定值.
为定值.


科目:高中数学 来源: 题型:
【题目】某沿海城市的海边有两条相互垂直的直线型公路l1、l2,海岸边界MPN近似地看成一条曲线段.为开发旅游资源,需修建一条连接两条公路的直线型观光大道AB,且直线AB与曲线MPN有且仅有一个公共点P(即直线与曲线相切),如图所示.若曲线段MPN是函数![]() 图象的一段,点M到l1、l2的距离分别为8千米和1千米,点N到l2的距离为10千米,以l1、l2分别为x、y轴建立如图所示的平面直角坐标系xOy,设点P的横坐标为p.
图象的一段,点M到l1、l2的距离分别为8千米和1千米,点N到l2的距离为10千米,以l1、l2分别为x、y轴建立如图所示的平面直角坐标系xOy,设点P的横坐标为p.
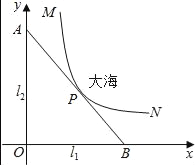
(1)求曲线段MPN的函数关系式,并指出其定义域;
(2)若某人从点O沿公路至点P观景,要使得沿折线OAP比沿折线OBP的路程更近,求p的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在直角坐标系![]() 中,点
中,点![]() 到抛物线
到抛物线![]() 的准线的距离为
的准线的距离为![]() ,点
,点![]() 是
是![]() 上的定点,
上的定点,![]() 、
、![]() 是
是![]() 上的两个动点,且线段
上的两个动点,且线段![]() 的中点
的中点![]() 在线段
在线段![]() 上.
上.
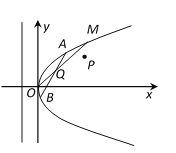
(1)抛物线![]() 的方程及
的方程及![]() 的值;
的值;
(2)当点![]() 、
、![]() 分别在第一、四象限时,求
分别在第一、四象限时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,且点
,且点![]() 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)当点![]() 在椭圆
在椭圆![]() 的图像上运动时,点
的图像上运动时,点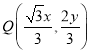 在曲线
在曲线![]() 上运动,求曲线
上运动,求曲线![]() 的轨迹方程,并指出该曲线是什么图形;
的轨迹方程,并指出该曲线是什么图形;
(3)过椭圆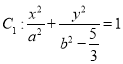 上异于其顶点的任意一点
上异于其顶点的任意一点![]() 作曲线
作曲线![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() 不在坐标轴上),若直线
不在坐标轴上),若直线![]() 在
在![]() 轴,
轴,![]() 轴上的截距分别为
轴上的截距分别为![]() 试问:
试问:![]() 是否为定值?若是,求出该定值;若不是,请说明理由.
是否为定值?若是,求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sinxcosx![]() cos2x+1
cos2x+1
(1)求f(x)的最小正周期和最大值,并写出取得最大值时x的集合;
(2)将f(x)的函数图象向左平移φ(φ>0)个单位后得到的函数g(x)是偶函数,求φ的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】狄利克雷函数为F(x) .有下列四个命题:①此函数为偶函数,且有无数条对称轴;②此函数的值域是
.有下列四个命题:①此函数为偶函数,且有无数条对称轴;②此函数的值域是![]() ;③此函数为周期函数,但没有最小正周期;④存在三点
;③此函数为周期函数,但没有最小正周期;④存在三点![]() ,使得△ABC是等腰直角三角形,以上命题正确的是( )
,使得△ABC是等腰直角三角形,以上命题正确的是( )
A.①②B.①③C.③④D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司要在一条笔直的道路边安装路灯,要求灯柱AB与底面垂直,灯杆BC与灯柱AB所在的平面与道路走向垂直,路灯C采用锥形灯罩,射出的管线与平面ABC部分截面如图中阴影所示,![]() 路宽AD=24米,设
路宽AD=24米,设![]()
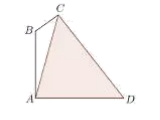
(1)求灯柱AB的高h(用![]() 表示);
表示);
(2)此公司应该如何设置![]() 的值才能使制作路灯灯柱AB和灯杆BC所用材料的总长度最小?最小值为多少?
的值才能使制作路灯灯柱AB和灯杆BC所用材料的总长度最小?最小值为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com