
【题目】如图是从成都某中学参加高三体育考试的学生中抽出的40名学生体育成绩(均为整数)的频率分布直方图,该直方图恰好缺少了成绩在区间[70,80)内的图形,根据图形的信息,回答下列问题: 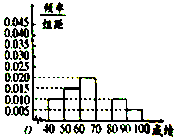
(1)求成绩在区间[70,80)内的频率,并补全这个频率分布直方图,并估计这次考试的及格率(60分及以上为及格);
(2)从成绩在[80,100]内的学生中选出三人,记在90分以上(含90分)的人数为X,求X的分布列及数学期望.
【答案】
(1)解:根据各组的频率和等于1知,
成绩在[70,80)内的频率为:
f4=1﹣(0.01×2+0.015+0.020+0.005)×10=0.4,
对应的小矩形的高为 ![]() =0.04,
=0.04,
补全频率分布直方图如图所示;
依题意,60分及以上的分数在第三、四、五、六段,
故其频率和为(0.02+0.04+0.01+0.005)×10=0.75,
∴估计学生成绩的及格率是75%
(2)解:成绩在[80,100]内的人数为(0.01+0.005)×10×40=6,
且在[80,90)和[90,100)内的人数分别为4人和2人;
∴X的可能取值为0、1、2,
计算P(X=0)= ![]() =
= ![]() ,
,
P(X=1)= ![]() =
= ![]() ,
,
P(X=2)= ![]() =
= ![]() ,
,
∴X的分布列为:
X | 0 | 1 | 2 |
P |
|
|
|
数学期望为E(X)=0× ![]() +1×
+1× ![]() +2×
+2× ![]() =1.
=1.
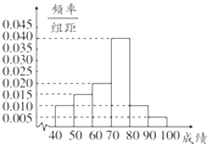
【解析】(1)根据各组的频率和为1求出成绩在[70,80)内的频率,计算对应小矩形的高,补全频率分布直方图,再计算60分及以上分数的频率和即可;(2)计算成绩在[80,90)和[90,100)内的人数,得X的可能取值,求出对应的概率值,写出X的分布列,计算数学期望.
【考点精析】认真审题,首先需要了解频率分布直方图(频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息),还要掌握离散型随机变量及其分布列(在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列)的相关知识才是答题的关键.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=4tanxsin( ![]() ﹣x)cos(x﹣
﹣x)cos(x﹣ ![]() )﹣
)﹣ ![]() .
.
(1)求f(x)的定义域与最小正周期;
(2)讨论f(x)在区间[﹣ ![]() ,
, ![]() ]上的单调性.
]上的单调性.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn , 且满足Sn=2﹣an , n=1,2,3,….
(1)求数列{an}的通项公式;
(2)若数列{bn}满足b1=1,且bn+1=bn+an , 求数列{bn}的通项公式;
(3)设cn=n(3﹣bn),求数列{cn}的前n项和为Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A是函数y=lg(6+5x﹣x2)的定义域,集合B是不等式x2﹣2x+1﹣a2≥0(a>0)的解集.p:x∈A,q:x∈B.
(1)若A∩B=,求a的取值范围;
(2)若¬p是q的充分不必要条件,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司租赁甲、乙两种设备生产A,B两类产品,甲种设备每天能生产A类产品5件和B类产品10件,乙种设备每天能生产A类产品6件和B类产品20件。已知设备甲每天的租赁费为200元,设备乙每天的租赁费为300元,现该公司至少要生产A类产品50件,B类产品140件,所需租赁费最少为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某上市股票在30天内每股的交易价格P(元)与时间t(天)组成有序数对(t,P),点(t,P)落在图中的两条线段上(如图).该股票在30天内(包括第30天)的日交易量Q(万股)与时间t(天)的函数关系式为Q=40﹣t(0≤t≤30且t∈N). 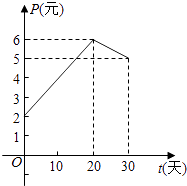
(1)根据提供的图象,求出该种股票每股的交易价格P(元)与时间t(天)所满足的函数关系式;
(2)用y(万元)表示该股票日交易额(日交易额=日交易量×每股的交易价格),写出y关于t的函数关系式,并求出这30天中第几天日交易额最大,最大值为多少.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com