
【题目】已知![]() ,求证:
,求证:![]() .
.
【答案】![]()
【解析】试题分析:
2α+β=α+(α+β),β=(α+β)-α,结合题意可知和两角和差正余弦公式即可证得题中的结论.
试题解析:
∵2α+β=α+(α+β),β=(α+β)-α,
∴sin(2α+β)=sin[(α+β)+α]=sin(α+β)cosα+cos(α+β)sinα,
而5sinβ=5sin[(α+β)-α]=5sin(α+β)cosα-5cos(α+β)sinα.
由已知得sin(α+β)cosα+cos(α+β)sinα=5sin(α+β)cosα-5cos(α+β)sinα.
∴2sin(α+β)cosα=3cos(α+β)sinα,
等式两边都除以cos(α+β)cosα,得2tan(α+β)=3tanα.


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,已知曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数,
为参数,![]() ).
).
(Ⅰ)当![]() 时,若曲线
时,若曲线![]() 上存在
上存在![]() 两点关于点
两点关于点![]() 成中心对称,求直线
成中心对称,求直线![]() 的参数方程;
的参数方程;
(Ⅱ)在以原点为极点,![]() 轴的正半轴为极轴的极坐标系中,极坐标方程为
轴的正半轴为极轴的极坐标系中,极坐标方程为![]() 的直线
的直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,若
两点,若![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,向量 ![]() =(a+b,sinA﹣sinC),且
=(a+b,sinA﹣sinC),且 ![]() =(c,sinA﹣sinB),且
=(c,sinA﹣sinB),且 ![]() ∥
∥ ![]() .
.
(1)求角B的大小;
(2)若a+c=8,求AC边上中线长的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=asin(x+ ![]() )﹣b(a>0)的最大值为2,最小值为0.
)﹣b(a>0)的最大值为2,最小值为0.
(1)求a、b的值;
(2)利用列表法画出函数在一个周期内的图象.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】要得到函数y=3cos(2x﹣ ![]() )的图象,可以将函数y=3sin2x的图象( )
)的图象,可以将函数y=3sin2x的图象( )
A.沿x轴向左平移 ![]() 单位
单位
B.沿x轴向右平移 ![]() 单位
单位
C.沿x轴向左平移 ![]() 单位
单位
D.沿x轴向右平移 ![]() 单位
单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两个班级均为40人,进行一门考试后,按学生考试成绩及 格与不及格进行统计,甲班及格人数为36人,乙班及格人数为24人.
(1) 根据以上数据建立一个![]() 的列联表;
的列联表;
(2) 试判断成绩与班级是否有关?
参考公式:![]() ,其中
,其中![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,已知a、b、c分别是三内角A、B、C所对应的边长,且b2+c2﹣a2=bc
(1)求角A的大小;
(2)若sin2A+sin2B=sin2C,试判断△ABC的形状并求角B的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知Sn是正项数列{an}的前n项和,且Sn= ![]() an2+
an2+ ![]() an﹣
an﹣ ![]()
(1)求数列{an}的通项公式;
(2)若an=2nbn , 求数列{bn}的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自选题:已知曲线C1: ![]() (θ为参数),曲线C2:
(θ为参数),曲线C2: 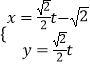 (t为参数).
(t为参数).
(1)指出C1 , C2各是什么曲线,并说明C1与C2公共点的个数;
(2)若把C1 , C2上各点的纵坐标都压缩为原来的一半,分别得到曲线C1′,C2′.写出C1′,C2′的参数方程.C1′与C2′公共点的个数和C与C2公共点的个数是否相同?说明你的理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com