
【题目】2017年,世界乒乓球锦标赛在德国的杜赛尔多夫举行.整个比赛精彩纷呈,参赛选手展现出很高的竞技水平,为观众奉献了多场精彩对决.图1(扇形图)和表1是其中一场关键比赛的部分数据统计.两位选手在此次比赛中击球所使用的各项技术的比例统计如图1.在乒乓球比赛中,接发球技术是指回接对方发球时使用的各种方法.选手乙在比赛中的接发球技术统计如表1,其中的前4项技术统称反手技术,后3项技术统称为正手技术.

图1
选手乙的接发球技术统计表
技术 | 反手拧球 | 反手搓球 | 反手拉球 | 反手拨球 | 正手搓球 | 正手拉球 | 正手挑球 |
使用次数 | 20 | 2 | 2 | 4 | 12 | 4 | 1 |
得分率 | 55% | 50% | 0% | 75% | 41.7% | 75% | 100% |
表1
(Ⅰ)观察图1,在两位选手共同使用的8项技术中,差异最为显著的是哪两项技术?
(Ⅱ)乒乓球接发球技术中的拉球技术包括正手拉球和反手拉球.从表1统计的选手乙的所有拉球中任取两次,至少抽出一次反手拉球的概率是多少?
(Ⅲ)如果仅从表1中选手乙接发球得分率的稳定性来看(不考虑使用次数),你认为选手乙的反手技术更稳定还是正手技术更稳定?(结论不要求证明)
【答案】(Ⅰ)正手搓球和反手拧球(Ⅱ)![]() (Ⅲ)正手技术更稳定.
(Ⅲ)正手技术更稳定.
【解析】试题分析:(Ⅰ)根据所给扇形图的数据可知,差异最为显著的是正手搓球和反手拧球两项技术.
(Ⅱ)根据表1的数据可知,选手乙的反手拉球2次,分别记为A,B,正手拉球4次,分别记为a,b,c,d.则从这六次拉球中任取两次,共15种结果,其中至少抽出一次反手拉球的共有9种,由古典概型概率公式可得概率
(Ⅲ)正手技术更稳定.
试题解析:
(Ⅰ)根据所给扇形图的数据可知,差异最为显著的是正手搓球和反手拧球两项技术.
(Ⅱ)根据表1的数据可知,选手乙的反手拉球2次,分别记为A,B,正手拉球4次,分别记为a,b,c,d.则从这六次拉球中任取两次,共15种结果,分别是:
AB, Aa,Ab, Ac, Ad, Ba, Bb,Bc, Bd, ab,ac, ad, bc, bd,cd.
其中至少抽出一次反手拉球的共有9种,分别是:
AB,Aa,Ab,Ac, Ad, Ba, Bb,Bc, Bd.
则从表1统计的选手乙的所有拉球中任取两次,至少抽出一次反手拉球的概率![]() .
.
(Ⅲ)正手技术更稳定.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
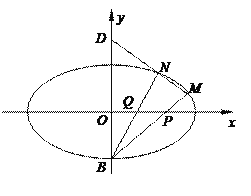
【题目】如图,在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的下顶点为
的下顶点为![]() ,点
,点![]() 是椭圆上异于点
是椭圆上异于点![]() 的动点,直线
的动点,直线![]() 分别与
分别与![]() 轴交于点
轴交于点![]() ,且点
,且点![]() 是线段
是线段![]() 的中点.当点
的中点.当点![]() 运动到点
运动到点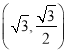 处时,点
处时,点![]() 的坐标为
的坐标为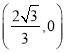 .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设直线![]() 交
交![]() 轴于点
轴于点![]() ,当点
,当点![]() 均在
均在![]() 轴右侧,且
轴右侧,且![]() 时,求直线
时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1, 在直角梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为线段
为线段![]() 的中点. 将
的中点. 将![]() 沿
沿![]() 折起,使平面
折起,使平面![]()
![]() 平面
平面![]() ,得到几何体
,得到几何体![]() ,如图2所示.
,如图2所示.
(1)求证: ![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司计划购买2台机器,该种机器使用三年后即被淘汰.机器有一易损零件,在购进机器时,可以额外购买这种零件作为备件,每个200元.在机器使用期间,如果备件不足再购买,则每个500元.现需决策在购买机器时应同时购买几个易损零件,为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数,得下面柱状图:

以这100台机器更换的易损零件数的频率代替1台机器更换的易损零件数发生的概率,记X表示2台机器三年内共需更换的易损零件数,n表示购买2台机器的同时购买的易损零件数.
(1)求X的分布列;
(2)若要求P(X≤n)≤0.5,确定n的最小值;
(3)以购买易损零件所需费用的期望值为决策依据,在n=19与n=20之中选其一,应选用哪个?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设S是实数集R的非空子集,若对任意x,y∈S,都有x+y,x-y,xy∈S,则称S为封闭集.下列命题:①集合S={a+b![]() |a,b为整数}为封闭集;②若S为封闭集,则一定有0∈S;③封闭集一定是无限集;④若S为封闭集,则满足STR的任意集合T也是封闭集.其中真命题是________.(写出所有真命题的序号)
|a,b为整数}为封闭集;②若S为封闭集,则一定有0∈S;③封闭集一定是无限集;④若S为封闭集,则满足STR的任意集合T也是封闭集.其中真命题是________.(写出所有真命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在“新零售”模式的背景下,某大型零售公司为推广线下分店,计划在![]() 市的
市的![]() 区开设分店.为了确定在该区开设分店的个数,该公司对该市已开设分店的其他区的数据作了初步处理后得到下列表格.记
区开设分店.为了确定在该区开设分店的个数,该公司对该市已开设分店的其他区的数据作了初步处理后得到下列表格.记![]() 表示在各区开设分店的个数,
表示在各区开设分店的个数, ![]() 表示这
表示这![]() 个分店的年收入之和.
个分店的年收入之和.
| 2 | 3 | 4 | 5 | 6 |
| 2.5 | 3 | 4 | 4.5 | 6 |
(Ⅰ)该公司已经过初步判断,可用线性回归模型拟合![]() 与
与![]() 的关系,求
的关系,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(Ⅱ)假设该公司在![]() 区获得的总年利润
区获得的总年利润![]() (单位:百万元)与
(单位:百万元)与![]() 之间的关系为
之间的关系为![]() ,请结合(Ⅰ)中的线性回归方程,估算该公司应在
,请结合(Ⅰ)中的线性回归方程,估算该公司应在![]() 区开设多少个分店,才能使
区开设多少个分店,才能使![]() 区平均每个分店的年利润最大?
区平均每个分店的年利润最大?
参考公式:
![]() ,
, 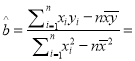
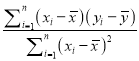 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来我国电子商务行业迎来发展的新机遇,2017年双11全天交易额达到1682亿元,为规范和评估该行业的情况,相关管理部门制定出针对电商的商品和服务的评价体系.现从评价系统中选出200次成功交易,并对其评价进行评价,对商品的好评率为0.6,对服务的好评率为0.75,其中对商品和服务都做出好评的交易为80次.
(1)完成关于商品和服务评价的![]() 列联表,判断能否在犯错误的概率不超过0.001的前提下,认为商品好评与服务好评有关?
列联表,判断能否在犯错误的概率不超过0.001的前提下,认为商品好评与服务好评有关?
(2)若将频率视为概率,某人在该购物平台上进行的3次购物中,设对商品和服务全为好评的次数为随机变量![]() :
:
①求对商品和服务全为好评的次数![]() 的分布列;
的分布列;
②求![]() 的数学期望和方差.
的数学期望和方差.
附:临界值表:

![]() 的观测值:
的观测值: 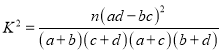 (其中
(其中![]() )
)
关于商品和服务评价的![]() 列联表:
列联表:

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2017·黄冈质检)设等比数列{an}的各项均为正数,公比为q,前n项和为Sn.若对任意的n∈N*,有S2n<3Sn,则q的取值范围是( )
A. (0,1] B. (0,2)
C. [1,2) D. (0, ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com