
【题目】已知函数![]() 的导函数为
的导函数为![]() ,且对任意的实数
,且对任意的实数![]() 都有
都有![]() (
(![]() 是自然对数的底数),且
是自然对数的底数),且![]() ,若关于
,若关于![]() 的不等式
的不等式![]() 的解集中恰有两个整数,则实数
的解集中恰有两个整数,则实数![]() 的取值范围是
的取值范围是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】
利用导数研究其单调性极值与最值并且画出图象即可得出.
∵f'(x)=e﹣x(2x+3)﹣f(x),
∴ex[f(′x)+f(x)]=2x+3,
∴exf(x)=x2+3x+c,
∵f(0)=1,
∴1=0+0+c,
解得c=1
∴f(x)=(x2+3x+1)e﹣x,
∴f′(x)=﹣(x2+x﹣2)e﹣x=﹣(x﹣1)(x+2)e﹣x.
令f′(x)=0,解得x=1或x=﹣2,
当x<﹣2或x>1时,f′(x)<0,函数f(x)单调递减,
当﹣2<x<1时,f′(x)>0,函数f(x)单调递减增,
可得:x=1时,函数f(x)取得极大值,x=﹣2时,函数f(x)取得极小值,
∵f(1)=![]() ,f(﹣2)=﹣e2<0,f(﹣1)=﹣e,f(0)=1>0,f(﹣3)=e3>0
,f(﹣2)=﹣e2<0,f(﹣1)=﹣e,f(0)=1>0,f(﹣3)=e3>0
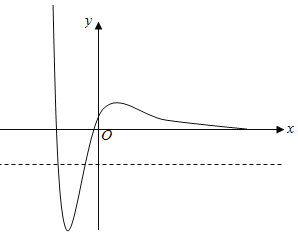
∴﹣e<m≤0时,f(x)﹣m<0的解集中恰有两个整数恰有两个整数﹣1,﹣2.
故m的取值范围是(﹣e,0],
故选:A.


科目:高中数学 来源: 题型:
【题目】下列命题正确的是( )
A. 幂函数的图象都经过![]() 、
、![]() 两点
两点
B. 当![]() 时,函数
时,函数![]() 的图象是一条直线
的图象是一条直线
C. 如果两个幂函数的图象有三个公共点,那么这两个函数一定相同
D. 如果幂函数为偶函数,则图象一定经过点![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,已知直线
轴正半轴为极轴,建立极坐标系,已知直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),曲线
为参数),曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程,并指出该曲线是什么曲线;
的直角坐标方程,并指出该曲线是什么曲线;
(2)若直线![]() 与曲线
与曲线![]() 的交点分别为
的交点分别为![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(原创,较难)椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() ,与y轴正半轴交于点B,若
,与y轴正半轴交于点B,若![]() 为等腰直角三角形,且直
为等腰直角三角形,且直![]() 线被圆
线被圆![]() 所截得的弦长为2.
所截得的弦长为2.
(1)求椭圆的方程;(2)直线l与椭圆交于点A、C,线段AC的中点为M,射线MO与椭圆交于点P,点O为![]() 重心,探求
重心,探求![]() 面积
面积![]() 是否为定值,若是求出这个值,若不是求
是否为定值,若是求出这个值,若不是求![]() 的取值范围
的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】通过随机询问50名性别不同的大学生是否爱好某项运动,得到如下的列联表,由![]() 得
得![]() 参照附表,得到的正确结论是( )
参照附表,得到的正确结论是( )
爱好 | 不爱好 | 合计 | |
男生 | 20 | 5 | 25 |
女生 | 10 | 15 | 25 |
合计 | 30 | 20 | 50 |
| 0.010 | 0.005 | 0.001 |
| 6.635 | 7.879 | 10.828 |
A.有99.5%以上的把握认为“爱好该项运动与性别有关”
B.有99.5%以上的把握认为“爱好该项运动与性别无关”
C.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
D.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某家具厂生产一种办公桌,每张办公桌的成本为100元,出厂单价为160元,该厂为鼓励销售商多订购,决定一次订购量超过100张时,每超过一张,这批订购的全部办公桌出厂单价降低1元.根据市场调查,销售商一次订购量不会超过160张.
(1)设一次订购量为![]() 张,办公桌的实际出厂单价为
张,办公桌的实际出厂单价为![]() 元,求
元,求![]() 关于
关于![]() 的函数关系式
的函数关系式![]() ;
;
(2)当一次性订购量![]() 为多少时,该家具厂这次销售办公桌所获得的利润
为多少时,该家具厂这次销售办公桌所获得的利润![]() 最大?其最大利润是多少元?(该家具厂出售一张办公桌的利润=实际出厂单价-成本)
最大?其最大利润是多少元?(该家具厂出售一张办公桌的利润=实际出厂单价-成本)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com