
分析 ①,函数y=sin(2x-$\frac{π}{3}$)的图象可以由y=sin2x的图象向右平移$\frac{π}{6}$个单位长度得到;
②,已知函数f(x)=(a2-a-1)x${\;}^{\frac{1}{a-2}}$为幂函数,则a2-a-1=1且a≠2⇒a=-1;
③,若扇形圆心角的弧度数为2,且扇形弧所对的弦长也是2,则扇形的半径为$\frac{1}{sin1}$,这个扇形的面积为$\frac{1}{2}×2×\frac{1}{si{n}^{2}1}$=$\frac{1}{si{n}^{2}1}$;
④,函数f(x)=lg|x|-sinx的零点个数就是y=lg|x|与 y=sinx的交点,画出两函数图象,根据图判定;
解答 解:对于①,函数y=sin(2x-$\frac{π}{3}$)的图象可以由y=sin2x的图象向右平移$\frac{π}{6}$个单位长度得到,故错;
对于②,已知函数f(x)=(a2-a-1)x${\;}^{\frac{1}{a-2}}$为幂函数,则a2-a-1=1且a≠2,⇒a=-1,故正确;
对于③,若扇形圆心角的弧度数为2,且扇形弧所对的弦长也是2,则扇形的半径为$\frac{1}{sin1}$,这个扇形的面积为$\frac{1}{2}×2×\frac{1}{si{n}^{2}1}$=$\frac{1}{si{n}^{2}1}$,故正确;
对于④,设函数f(x)=lg|x|-sinx的零点个数就是y=lg|x|与 y=sinx的交点,如图所示,故正确;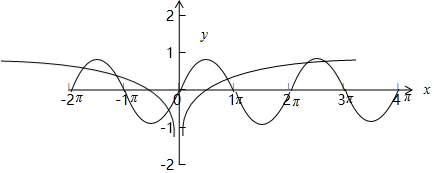
故答案为:②③④
点评 本题考查了命题真假的判定,涉及到了大量的函数知识,属于基础题.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 设抛物线E:y2=2px(p>0)上的点M(x0,4)到焦点F的距离|MF|=$\frac{5}{4}$x0.
设抛物线E:y2=2px(p>0)上的点M(x0,4)到焦点F的距离|MF|=$\frac{5}{4}$x0.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
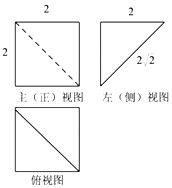
| A. | $\frac{4}{3}$ | B. | $\frac{8}{3}$ | C. | $\frac{{8\sqrt{2}}}{3}$ | D. | $\frac{{4\sqrt{2}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
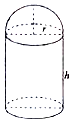 某化工厂拟建一个下部为圆柱,上部为半球的容器(如图,圆柱高为h,半径为r,不计厚度,单位:米),按计划容积为72π立方米,且h≥2r,假设其建造费用仅与表面积有关(圆柱底部不计),已知圆柱部分每平方米的费用为2千元,半球部分每平方米4千元,设该容器的建造费用为y千元.
某化工厂拟建一个下部为圆柱,上部为半球的容器(如图,圆柱高为h,半径为r,不计厚度,单位:米),按计划容积为72π立方米,且h≥2r,假设其建造费用仅与表面积有关(圆柱底部不计),已知圆柱部分每平方米的费用为2千元,半球部分每平方米4千元,设该容器的建造费用为y千元.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com