
 18、ABCD是矩形,四个顶点在平面α内的射影分别为A′,B′,C′,D′,直线A′B′与C′D′不重合.
18、ABCD是矩形,四个顶点在平面α内的射影分别为A′,B′,C′,D′,直线A′B′与C′D′不重合.

科目:高中数学 来源: 题型:
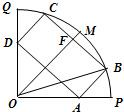 如图所示,某市政府决定在以政府大楼O为中心,正北方向和正东方向的马路为边界的扇形地域内建造一个图书馆.为了充分利用这块土地,并考虑与周边环境协调,设计要求该图书馆底面矩形的四个顶点都要在边界上,图书馆的正面要朝市政府大楼.设扇形的半径OM=R,∠MOP=45°,OB与OM之间的夹角为θ.
如图所示,某市政府决定在以政府大楼O为中心,正北方向和正东方向的马路为边界的扇形地域内建造一个图书馆.为了充分利用这块土地,并考虑与周边环境协调,设计要求该图书馆底面矩形的四个顶点都要在边界上,图书馆的正面要朝市政府大楼.设扇形的半径OM=R,∠MOP=45°,OB与OM之间的夹角为θ.查看答案和解析>>
科目:高中数学 来源: 题型:
 在四棱锥P-ABCD中,PA⊥底面ABCD,底面四边形ABCD是矩形,且AD=3AB,点E是底面的边BC上的动点,设
在四棱锥P-ABCD中,PA⊥底面ABCD,底面四边形ABCD是矩形,且AD=3AB,点E是底面的边BC上的动点,设| BE |
| BC |
| A、0个 | B、1个 | C、2个 | D、3个 |
查看答案和解析>>
科目:高中数学 来源:必修二训练数学北师版 北师版 题型:047
如图所示,四边形ABCD是矩形,四个顶点在平面α的同一侧,四个顶点在α内的射影分别为![]() 、
、![]() 、
、![]() 、
、![]() ,且它们不共线,求证:四边形
,且它们不共线,求证:四边形![]()
![]()
![]()
![]() 是平行四边形.
是平行四边形.

查看答案和解析>>
科目:高中数学 来源: 题型:
(1)求证:A′B′C′D′是一平行四边形;
(2)在什么条件下,A′B′C′D′也是矩形?并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com